题目内容
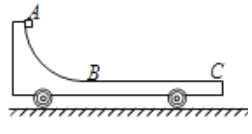
【题目】如图,水平光滑地面上停放着一质量为M的小车,其左侧有半径为R的四分之一光滑圆弧轨道AB，轨道最低点B与长为L的水平轨道BC相切,整个轨道处于同一竖直平面内。将质量为m的物块(可视为质点)从A点无初速释放,物块沿轨道滑行至轨道末端C处恰好没有滑出,设重力加速度为g,空气阻力可怎略不计。关于物块从A位置运动至C位置的过程中,下列说法正确的（ ）
A. 小车和物块构成的系统动量守恒
B. 摩擦力对物块和轨道所做的功的代数和为-mgR
C. 小车在全过程中运动的最大位移为
D. 小车运动过程中的最大速度为
【答案】BD
【解析】
系统所受合外力为零时，系统动量守恒；
由动能定理或机械能守恒定律求出物块滑到B点时的速度，然后由动量守恒定律求出物块与小车的共同速度，即为最大速度。
A项：在物块从A位置运动到B位置过程中，小车和物块构成的系统在受到的合力不为零，系统动量不守恒，但在水平方向上动量守恒，故A错误；
B项：由功能关系可知，摩擦力对物块和轨道所做的功的代数和的绝对值为因摩擦产生的内能即损失的机械能，由系统水平方向动量守恒可知，最后A物块和小车都静止，由能量守恒可知，损失的机械能为mgR，故B正确；
C项：由系统水平方向动量守恒和“人船模型”可知，
，
，解得：
，故C错误；
D项：当A物块运动到B点时，小车的速度最大，由水平方向动量守恒得：
，由机械能守恒得：
，联立解得：
，故D正确。
故应选：BD。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
