题目内容
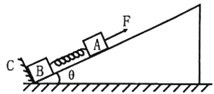
【题目】如图所示,C是放在光滑的水平面上的一块木板,木板的质量为3m,在木板的上面有两块质量均为m的小木块A和B,它们与木板间的动摩擦因数均为μ.最初木板静止,A、B两木块同时以方向水平向右的初速度v0和2v0在木板上滑动,木板足够长,A、B始终未滑离木板.求:
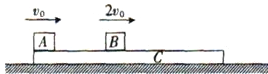
(1)木块B从刚开始运动到与木板C速度刚好相等的过程中,木块B所发生的位移;
(2)木块A在整个过程中的最小速度;
(3)整个过程中,A、B两木块相对于滑板滑动的总路程是多少?
【答案】(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]()
【解析】
试题分析:(1)木块A先做匀减速直线运动,后做匀加速直线运动;木块B一直做匀减速直线运动;木板C做两段加速度不同的匀加速直线运动,直到A、B、C三者的速度相等为止,设为v1.对A、B、C三者组成的系统,由动量守恒定律得:mv0+2mv0=(m+m+3m)v1
解得:v1=0.6 v0
对木块B运用动能定理,有:![]()
解得:![]()
(2)设木块A在整个过程中的最小速度为v′,所用时间为t,由牛顿第二定律:
对木块A:a1=μmg/m=μg,对木块C:a2=2μmg/3m=2μg/3,
当木块A与木板C的速度相等时,木块A的速度最小,因此有:v0-μgt=(2μg/3)t
解得t=3v0/(5μg)
木块A在整个过程中的最小速度为:v′=v0-a1t=2v0 /5.
(3)Q总=Q1+Q2 = fs相1+fs相2=ΔEk损
所以![]()

 阅读快车系列答案
阅读快车系列答案【题目】某同学利用下述装置对轻质弹簧的弹性势能进行研究,一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触不固连;弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示。向左推小球,使弹簧压缩一段距离后由静止释放;小球离开桌面后落到水平地面,通过测量和计算,可求得弹簧被压缩后的弹性势能。 回答下列问题:
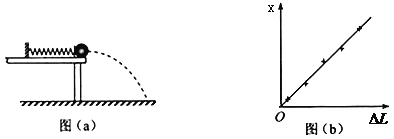
(1)本实验中可认为,弹簧被压缩后的弹性势能EP与小球抛出时的动能Ek相等,已知重力加速度大小为g,为求得Ek,至少需要测量下列物理量中的_______(填正确答案标号)
A.小球的质量m |
B.小球抛出点到落地点的水平距离x |
C.桌面到地面的高度h |
D.弹簧的压缩量△L |
E.弹簧原长L0
(2)用所选取的测量量和已知量表示Ek,得Ek=_____________
(3)图(b)中的直线是实验测量得到的x-△L图线,从理论上可推出,如果h不变,m增加,x-△L图线的斜率会________(填“增大”、“减小”或“不变”);如果m不变,h增加,x-△L图线的斜率会________(填“增大”、“减小”或“不变”)。由图(b)中给出的直线关系和Ek的表达式可知,Ep与△L的_______次方成正比。