题目内容
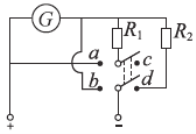
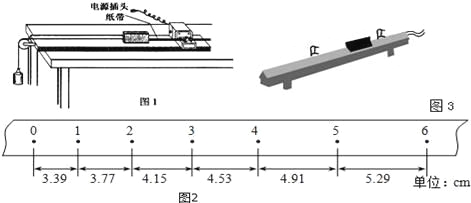
【题目】如图甲所示，一刚性矩形金属线框从高处自由下落，刚好匀速进入一匀强磁场区域，然后穿出磁场区域，已知线圈质量为m，电阻为R，长为l1，宽为l2，磁感应强度为B，磁场区域高度为d，假设线框运动过程中不翻转，整个过程不计空气阻力。
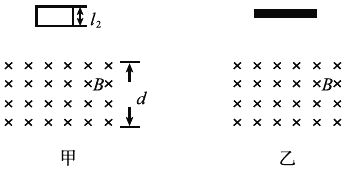
（1）若l2<d，试计算线框刚进入磁场时的速度大小，同时分析线框完全在磁场中做何种运动？
（2）若l2=d，试分析线框刚进入磁场到刚好完全离开磁场的过程中能量是如何转化的？通过分析、推导说明此过程中能量转化是守恒的。
（3）若将线框改为长度为a的金属棒，如图乙所示，金属棒由静止释放进入磁场，假设金属棒能保持水平状态穿过磁场，分析说明金属棒在磁场中产生感应电动势的原因并推导感应电动势E与瞬时速度v的关系式。
【答案】（1）线框做匀速直线运动；（2）见解析；（3）E=Bav。。
【解析】
试题分析：（1）线框匀速进入磁场，重力等于安培力，mg=BIl1
由关系式：I=
，E=Bl1v，可得v=
，
分析：线框匀速进入磁场后磁通量不变，因此电流消失不受安培力只受重力，线框做匀速直线运动。
（2）动能不变，重力势能转化为电能，电能转化不焦耳热，线框穿过磁场过程：由于保持匀速动能不变，重力势能减少了2mgl2
线框因发热产生的焦耳热为Q=I2Rt，有关系式：I= ，E=Bl1v，t=
，mg=BIl1；
带入可得：Q=2mgl2，这个过程重力势能完全转化为焦耳热。
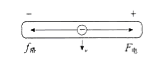
（3）金属棒中自由电子因在磁场中运动受洛伦兹力的作用向一端移动，两端出现等量异种电荷，这是产生电动势的本质原因；
电场力等于洛伦兹力：qE=qvB，又因U=Bav，故断路时电压等于电动势：E=Bav。
练习册系列答案
相关题目
