题目内容
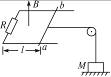
如图4-3-22所示,一对杂技演员(都视为质点)乘秋千(秋千绳处于水平位置)从A点由静止出发绕O点下摆,当摆到最低点B时,女演员在极短时间内将男演员沿水平方向推出,然后自已刚好能回到高处A.男演员落地点C与O点的水平距离为s,秋千的质量不计,秋千的摆长为R , C点比O点低5R.已知男演员质量m1,求:(1)女演员的质量m2;
(2)女演员将男演员推出的过程中所做的总功.

图4-3-22
思路点拨:该题综合考查圆周运动、平抛运动、动量守恒、机械能守恒和动能定理.两人乘秋千从A到B共同运动的过程中机械能守恒,可求出最低点的速度v0,在最低点女演员在极短时间内将男演员沿水平方向推出,动量守恒,女演员恰好回到A点,由机械能守恒可求出女演员在B点的速度v2,由平抛运动规律可得出男演员在B点的速度v1,由动量守恒即可求出女演员的质量m2.而求女演员将男演员推出的过程中所做的总功,无法直接利用功的公式求解,只能用动能定理得出.
解析:(1)设分离前男女演员在秋千最低点B的速度为v0,由机械能守恒定律
(m1+m2)gR=![]() (m1+m2)v02 ①
(m1+m2)v02 ①
设刚分离时男演员速度的大小为v1,方向与v0相同;女演员速度的大小为v2,方向与v0相反,由于动量守恒,
(m1+m2)v0=m1v1-m2v2 ②
分离后,男演员做平抛运动,设男演员从被推出到落在C点所需的时间为t,根据题给条件,由平抛运动规律,h=4R=![]() gt2 s=v1t ③
gt2 s=v1t ③
根据题给条件,女演员刚好回到A点,由机械能守恒定律,m2gR=![]() m2v22 ④
m2v22 ④
联立①②③④可解得:m2=![]() .
.
(2)女演员将男演员推出的过程中所做的总功,由动能定理得
W=![]() m1(v12-v02)=
m1(v12-v02)= ![]() m1(
m1(![]() -2Rg).
-2Rg).
答案:(1)![]()
(2)![]() m1(
m1(![]() -2Rg)
-2Rg)

练习册系列答案
相关题目