题目内容
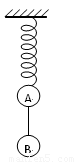
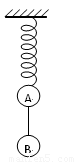
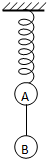如图所示，轻弹簧的下端系着A、B两球，mA=100g，mB=500g，系统静止时弹簧伸长x=15cm，未超出弹性限度．若剪断A、B间的细绳，则A在竖直方向做简谐运动，求：（1）A的振幅多大？
（2）A球的最大加速度多大？（g取10m/s2）
分析：先研究AB两球，由平衡关系要得出劲度系数；刚剪断细线时小球的加速度最大，此处相当于是小球到达简谐运动的振幅处．
解答：解：（1）只挂A球时弹簧伸长量由F=kx
得x1=
挂A、B两物体时有：kx=（mA+mB）g；
k=
=40N/m
剪断A、B间细线后，A球静止悬挂时的弹簧的伸长量为xA=
=0.025m
弹簧下端的这个位置就是A球振动中的平衡位置．
悬挂B球后又剪断细线，相当于用手把A球下拉后又突然释放，刚剪断细线时弹簧比静止悬挂A球多伸长的长度就是振幅，
即A=x-xA=15cm-2.5cm=12.5cm
（2）振动中A球的最大加速度为最大加速度为：
amax=
=
×10m/s2=50m/s2
答：（1）最大振幅为12.5cm；
（2）最大加速度为50m/s2．
得x1=
| mAg |
| k |
挂A、B两物体时有：kx=（mA+mB）g；
k=
| (mA+mB)g |
| x |
剪断A、B间细线后，A球静止悬挂时的弹簧的伸长量为xA=
| mAg |
| k |
弹簧下端的这个位置就是A球振动中的平衡位置．
悬挂B球后又剪断细线，相当于用手把A球下拉后又突然释放，刚剪断细线时弹簧比静止悬挂A球多伸长的长度就是振幅，
即A=x-xA=15cm-2.5cm=12.5cm
（2）振动中A球的最大加速度为最大加速度为：
amax=
| mBg |
| mA |
| 500 |
| 100 |
答：（1）最大振幅为12.5cm；
（2）最大加速度为50m/s2．
点评：解决简谐运动的题目应注意找出平衡位置，找出了平衡位置即能确定振幅及最大加速度．
练习册系列答案
相关题目
