Question

【题目】如图，一粗细均匀的细管开口向上竖直放置，管内有一段高度为2.0cm的水银柱，水银柱下密封了一定量的理想气体，水银柱上表面到管口的距离为2.0cm。若将细管倒置，水银柱下表面恰好位于管口处，且无水银滴落，管内气体温度与环境温度相同。已知大气压强为76cmHg，环境温度为296K。

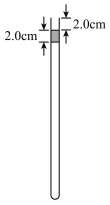
（1）求细管的长度；

（2）若在倒置前，缓慢加热管内被密封的气体，直到水银柱的上表面恰好与管口平齐为止，求此时密封气体的温度。

Answer 1

【答案】（1）41cm；（2）312K

【解析】

以“液柱”为模型，通过对气体压强分析，利用玻意耳定律和盖-吕萨克定律求得细管长度和温度，找准初末状态、分析封闭气体经历的变化时关键。易错点：误把气体长度当成细管长度。

（1）设细管的长度为l，横截面的面积为S，水银柱高度为h；初始时，设水银柱上表面到管口的距离为h，被密封气体的体积为V，压强为p；细管倒置时，气体体积为V1，压强为p1。由玻意耳定律有

pV=p1V1①

由力的平衡条件有

p=p0–ρgh③

式中，p、g分别为水银的密度和重力加速度的大小，p0为大气压强。由题意有

V=S（L–h1–h）④

V1=S（L–h）⑤

由①②③④⑤式和题给条件得

L=41cm⑥

（2）设气体被加热前后的温度分别为T0和T，由盖–吕萨克定律有

⑦

由④⑤⑥⑦式和题给数据得

T=312K⑧