题目内容
3. 2015年4月24日“哈勃空间望远镜”在太空服役满25周年.已知“哈勃空间望远镜”质量为m,轨道距地面高度为h,地球半径为R,地球表面的重力加速度为g.“哈勃空间望远镜”运行的过程可视作匀速圆周运动,则下列说法正确的是( )
2015年4月24日“哈勃空间望远镜”在太空服役满25周年.已知“哈勃空间望远镜”质量为m,轨道距地面高度为h,地球半径为R,地球表面的重力加速度为g.“哈勃空间望远镜”运行的过程可视作匀速圆周运动,则下列说法正确的是( )| A. | 哈勃空间望远镜运行的高度越高,运动速度越大 | |
| B. | 哈勃空间望远镜的运行时周期为T=$\frac{2π(R+h)}{R}$$\sqrt{\frac{R+h}{g}}$ | |
| C. | 哈勃空间望远镜在运行轨道上的向心加速度为a=($\frac{R+h}{R}$)2g | |
| D. | 由于地球质量未知,无法计算出哈勃空间望远镜与地球间的万有引力 |
分析 地球表面重力与万有引力相等,望远镜绕地球圆周运动由万有引力提供圆周运动向心力据此分析.
解答 解:A、据$G\frac{mM}{(R+h)^{2}}=m\frac{{v}^{2}}{R+h}$可得$v=\sqrt{\frac{GM}{R+h}}$地球质量一定,可知高度越高卫星运行速度越小,故A错误;
B、据$G\frac{Mm}{{R}^{2}}=mg$和$G\frac{mM}{(R+h)^{2}}=m(R+h)\frac{4{π}^{2}}{{T}^{2}}$可得望远镜周期T=$\sqrt{\frac{4{π}^{2}(R+h)^{3}}{g{R}^{2}}}=\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$,可得B正确;
C、据$G\frac{Mm}{{R}^{2}}=mg$和$G\frac{mM}{(R+h)^{2}}=ma$可得望远镜的向心加速度a=$({\frac{R}{R+h})}^{2}g$,故C错误;
D、根据万有引力与地球表面重力相等,可以由重力加速度和地球半径求得地球质量,故D错误.
故选:B.
点评 在星球表面重力与万有引力相等和万有引力提供圆周运动向心力这是解决万有引力应用问题的主要列式原理.

练习册系列答案
相关题目
13.光在某种介质的传播速度是真空中的一半,在光从该介质射向真空时,发生全反射的临界角是( )
| A. | 15° | B. | 30° | C. | 60° | D. | 65° |
14.光在科学技术、生产和生活中有着广泛的应用,下列选项说法正确的是( )
| A. | 观看“3D电影”所戴的眼镜镜片为偏振片 | |
| B. | 光学镜头上的增透膜是利用光的全反射现象 | |
| C. | 树叶上的小水珠看起来特别亮,这是光的干涉现象 | |
| D. | 太阳光下的肥皂泡呈现出彩色条纹,这是光的衍射现象 |
11.下列物理量为矢量的是( )
| A. | 路程 | B. | 时间 | C. | 质量 | D. | 重力 |
18.小刘同学用铅笔、细线把一个钩码按如图所示的方式悬挂起来,中指和手掌感受到的作用力分别为( )


| A. | 压力,拉力 | B. | 压力,压力 | C. | 拉力,拉力 | D. | 拉力,压力 |
8.下列各物理量属于矢量的是( )
| A. | 弹力 | B. | 功 | C. | 能量 | D. | 时间 |
15.如图所示,A、B是地球上的两点,其中A位于赤道上,B位于北纬60°的位置,则下列说法正确的( )
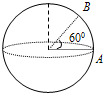

| A. | A、B两点的角速度相等 | B. | A、B两点的周期不相等 | ||
| C. | A、B两点的向心加速度aA:aB=2:1 | D. | A、B两点的线速度vA:vB=1:2 |
12.如图为一物体做直线运动的位移-时间图象,A,B,C,D为四个不同的时刻,其中与OA段平均速度相等的是( )
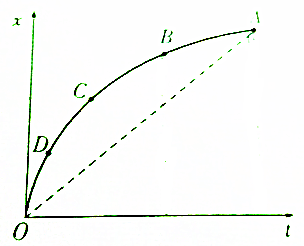

| A. | CD段的平均速度 | B. | B点的瞬时速度 | C. | C点的瞬时速度 | D. | AB段的平均速度 |