Question

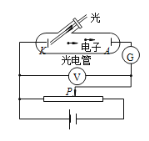
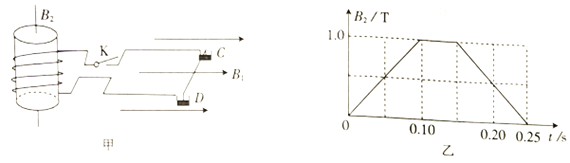
【题目】如图甲所示，质量为0.01kg、长为0.2m的水平金属细杆CD的两头分别放置在两水银槽的水银中，水银槽所在空间存在磁感应强度大小B1=10T、方向水平向右的匀强磁场，且杆CD与该匀强磁场垂直。有一匝数为100、面积为0.01m2的线圈通过开关K与两水银槽相连。线圈处于与线圈平面垂直、沿竖直方向的匀强磁场中，其磁感应强度B2随时间t变化关系如图乙所示。在t=0.20s时闭合开关K，细杆瞬间弹起(可认为安培力远大于重力)，弹起的最大高度为0.2m。不计空气阻力和水银的黏滞作用，不考虑细杆落回水槽后的运动，重力加速度g=10m/s2，下列说法正确的是

A. 磁感应强度B2的方向竖直向上

B. t=0.05s时，线圈中的感应电动势大小为10V

C. 细杆弹起过程中，细杆所受安培力的冲量大小为0.01N·s

D. 开关K闭合后，通过CD的电荷量为0.01C

Answer 1

【答案】ABD

【解析】

由法拉第电磁感应定律可以求出感应电动势，由左手定则可以判断出感应电流方向；然后用安培定则判断出线圈中感应电流磁场的方向，最后应用楞次定律判断磁感应强度的方向。在t=0.20s时闭合开关K，CD杆向上做竖直上抛运动，应用竖直上抛运动规律可以求出其获得的初速度，由动量定理求出细框受到的安培力，然后由电流定义式的变形公式求出电荷量。

A、细杆CD所受安培力方向竖直向上，由左手定则可知，电流方向为：C→D，由安培定则可知感应电流的磁场方向竖直向上，由图示图象可知，在0.20-0.25s内穿过线圈的磁通量减少，由楞次定律可知，磁感应强度B2方向：竖直向上，故A正确。

B、由图示图象可知，0～0.10s内：=BS=（1-0）×0.01=0.01Wb，0～0.10s线圈中的感应电动势大小：E=n=100V=10V，即0.15s时，线圈中的感应电动势大小为10V，故B正确。

C、细杆弹起瞬间的速度，v==m/s=2m/s，在t=0.20s时，细杆所受安培力的冲量(可认为安培力远大于重力)I=mv=0.01Ns=0.02Ns，故C错误。

D、开关K闭合后，对CD杆由动量定理得：B1ILt=mv-0，电荷量：Q=It，解得通过CD的电荷量：Q=It===C=0.01C，故D正确。

故选：ABD