题目内容
 如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取
如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取| 2 |
(1)小球经过B、D两个位置时对轨道的压力分别多大?
(2)小球从D点飞出后落到水平轨道的位置与B点相距多远?
分析:(1)小球经过D点时,由重力和轨道弹力的合力提供向心力,由牛顿第二定律求出小球经过D点时受到的弹力和速度.小球从B到D的过程,只有重力做功,其机械能守恒,根据机械能守恒定律求出小球经过B点的速度,再牛顿运动定律求解小球经过B点对轨道的压力.
(2)小球从D点飞出后做平抛运动,竖直方向做自由落体运动,由高度2R求出时间.水平方向做匀速直线运动,由公式x=vDt求出小球落到水平轨道的位置与B点的距离.
(2)小球从D点飞出后做平抛运动,竖直方向做自由落体运动,由高度2R求出时间.水平方向做匀速直线运动,由公式x=vDt求出小球落到水平轨道的位置与B点的距离.
解答:解:
(1)D点:根据牛顿第二定律得,FD+mg=maD,代入解得FD=7N.
由牛顿第三定律得,小球经过D时对轨道的压力大小为7N,方向竖直向上.
由aD=m
,得到vD=
=
=3m/s.
小球从B到D过程,由机械能守恒定律得
2mgR+
m
=
m
代入解得 vB=
=
=
m/s
B点:根据牛顿第二定律得,FB-mg=m
代入解得 FB=m(g+
)=0.2×(10+
)=19N
由牛顿第三定律得,小球经过B时对轨道的压力大小为19N,方向竖直向下.
(2)小球从D点飞出以vD=3m/s的初速度做平抛运动.
竖直方向:2R=
gt2
水平方向:x=vDt
联立上两式解得 x=0.84m
答:(1)小球经过B、D两个位置时对轨道的压力分别为19N和7N;
(2)小球从D点飞出后落到水平轨道的位置与B点相距0.84m.
(1)D点:根据牛顿第二定律得,FD+mg=maD,代入解得FD=7N.
由牛顿第三定律得,小球经过D时对轨道的压力大小为7N,方向竖直向上.
由aD=m
| ||
| R |
| aDR |
| 4.5×10 |
小球从B到D过程,由机械能守恒定律得
2mgR+
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
| v | 2 B |
代入解得 vB=
|
| 32+4×10×0.2 |
| 17 |
B点:根据牛顿第二定律得,FB-mg=m
| ||
| R |
代入解得 FB=m(g+
| ||
| R |
| 17 |
| 0.2 |
由牛顿第三定律得,小球经过B时对轨道的压力大小为19N,方向竖直向下.
(2)小球从D点飞出以vD=3m/s的初速度做平抛运动.
竖直方向:2R=
| 1 |
| 2 |
水平方向:x=vDt
联立上两式解得 x=0.84m
答:(1)小球经过B、D两个位置时对轨道的压力分别为19N和7N;
(2)小球从D点飞出后落到水平轨道的位置与B点相距0.84m.
点评:本题整合了牛顿运动定律、机械能守恒定律、平抛运动等知识,中等难度.抓住圆周运动的向心力是由指向圆心的合力提供.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取
如图所示,竖直的半圆型光滑轨道与水平轨道相切,轨道半径R=0.2m.质量m=0.2kg的小球以某一速度正对半圆型轨道运动,B、D两点分别是半圆轨道的最低点和最高点,小球经过B点的速度为vB=5m/s,达到D点时加速度的大小为4.5g,求:(取 =1.4 )
=1.4 )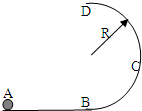

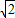 =1.4 )
=1.4 )