题目内容
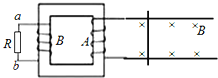
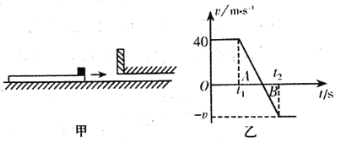
【题目】工厂某些产品出厂要进行碰撞实验。如图所示为一个理想的碰撞实验装置:一长薄板置于光滑水平地面上,薄板右端放置一物体,在薄板右方有一光滑通道,通道上方固定一个竖直障碍物,如图甲所示。从某一时刻开始,物体与薄板一起以共同速度向右运动,在另一时刻,物体与竖直障碍物发生碰撞(碰撞时间极短),而薄板可以沿通道运动。碰撞前后物体速度大小不变,方向相反。运动过程中物体始终未离开薄板。已知薄板运动的v-t图线如图乙所示,物体与薄板间的动摩擦因数为=0.4,物体的质量是薄板质量的15倍,重力加速度大小取g=10m/s2。求:
(1)物体相对薄板滑行的距离和图乙中速度v的大小;
(2)图乙中t2与t1的差值和两个三角形A、B的面积之差。
【答案】(1)v=35m/s,L=50m;(2)1.25s,3.125m
【解析】
考察碰撞中的动能定理和动量守恒。
根据图像可以判定:碰撞前物体与薄板共同速度为v0=40m/s,碰撞后物体速度水平向左,大小也是v0=40m/s,薄板速度大小方向不变。根据图像又知物体与薄板最后又共速,速度大小为v,方向向左
(1)设薄板的质量为m,物体的质量为M,物体相对木板滑行的距离为L,对物体和薄板组成的系统:从和竖直障碍物碰后到二者共速,取向左的方向为正方向,由动量守恒定律得
![]()
由能量守恒定律得
![]()
解得v=35m/s,L=50m。
(2)图乙中时间差(t2 - t1),是物体在薄板上相对薄板滑动的时间; 图乙中的两个三角形A、B的面积之差,是薄板在时间差(t2 - t1)内对地的位移大小。
设在图乙中的时间差(t2 - t1)内,薄板对地的位移大小为x,设t2 - t1=t,
对物体在薄板上相对木板滑动的过程中:
对物体:取向左的方向为正方向,由动量定理得
![]()
解得t=1.25s;
对薄板,由动能定理得
![]()
解得x=3.125m