题目内容
 (2012?丰台区一模)如图所示,在竖直平面内放置一长为L的薄壁玻璃管,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管右边的空间存在着匀强电场与匀强磁场的复合场.匀强磁场方向垂直于纸面向外,磁感应强度为B;匀强电场方向竖直向下 电场强度大小为
(2012?丰台区一模)如图所示,在竖直平面内放置一长为L的薄壁玻璃管,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管右边的空间存在着匀强电场与匀强磁场的复合场.匀强磁场方向垂直于纸面向外,磁感应强度为B;匀强电场方向竖直向下 电场强度大小为| mg | q |
(1)小球从玻璃管b端滑出时速度的大小.
(2)从玻璃管进入磁场至小球从b端滑出的过程中,外力F随时间t变化的关系.
(3)通过计算画出小球离开玻璃管后的运动轨迹.
分析:(1)分析小球在管中受力情况,由牛顿第二定律求出加速度.运用运动的分解法,研究小球在竖直方向的运动,由速度位移关系式求出小球从玻璃管b端滑出时竖直方向的分速度大小,再与水平方向速度合成求解小球从玻璃管b端滑出时速度的大小.
(2)玻璃管向右匀速运动,根据平衡条件求解外力F随时间t变化的关系.
(3)小球进入磁场后由洛伦兹力提供向心力,由牛顿第二定律求出半径,根据数学知识研究小球的偏向角,再画出轨迹.
(2)玻璃管向右匀速运动,根据平衡条件求解外力F随时间t变化的关系.
(3)小球进入磁场后由洛伦兹力提供向心力,由牛顿第二定律求出半径,根据数学知识研究小球的偏向角,再画出轨迹.
解答:解:(1)由题意可知:E=
,则有qE=mg,电场力与重力平衡,小球在管子中运动的加速度为:
a=
=
.
设小球从玻璃管b端滑出时竖直方向的分速度大小为vy,则: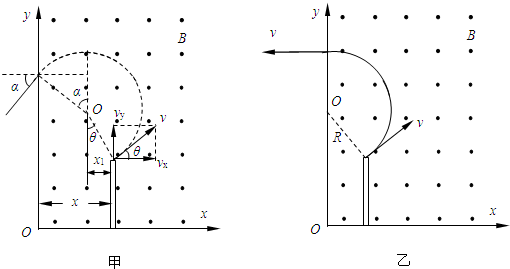
=2aL
所以小球从玻璃管b端滑出时速度的大小为:
v=
=
(2)玻璃管向右匀速运动,则有
F=Fx=Bvyq
又:vy=at=
t
则外力F随时间t变化的关系:F=
t.
(3)设小球在管中运动时间为t,小球在磁场中做圆周运动的半径为R,轨迹如图1所示.
t时间内玻璃管运动的距离为:x=v0t
根据牛顿第二定律得:qvB=m
得:R=
由几何关系有:sinα=
=
得:x1=
R=
?
=v0t=x
可得:sinα=0,α=0
即小球飞离磁场时速度方向垂直磁场左边界向左,则小球的运动轨迹如图2所示.
答:
(1)小球从玻璃管b端滑出时速度的大小为
.
(2)从玻璃管进入磁场至小球从b端滑出的过程z中,外力F随时间t变化的关系为F=
t.
(3)画出小球离开玻璃管后的运动轨迹如图2所示.
| mg |
| q |
a=
| Fy |
| m |
| Bv0q |
| m |
设小球从玻璃管b端滑出时竖直方向的分速度大小为vy,则:

| v | 2 y |
所以小球从玻璃管b端滑出时速度的大小为:
v=
|
|
(2)玻璃管向右匀速运动,则有
F=Fx=Bvyq
又:vy=at=
| Bv0q |
| m |
则外力F随时间t变化的关系:F=
| B2v0q2 |
| m |
(3)设小球在管中运动时间为t,小球在磁场中做圆周运动的半径为R,轨迹如图1所示.
t时间内玻璃管运动的距离为:x=v0t
根据牛顿第二定律得:qvB=m
| v2 |
| R |
得:R=
| mv |
| qB |
由几何关系有:sinα=
| x-x1 |
| R |
| x1 |
| R |
| vy |
| v |
得:x1=
| vy |
| v |
| Bv0qt |
| mv |
| mv |
| qB |
可得:sinα=0,α=0
即小球飞离磁场时速度方向垂直磁场左边界向左,则小球的运动轨迹如图2所示.
答:
(1)小球从玻璃管b端滑出时速度的大小为
|
(2)从玻璃管进入磁场至小球从b端滑出的过程z中,外力F随时间t变化的关系为F=
| B2v0q2 |
| m |
(3)画出小球离开玻璃管后的运动轨迹如图2所示.
点评:本题小球在重力、电场力、洛伦兹力作用下的运动,采用非常规的运动分解法.要注意洛伦兹力大小F=qvB,v应是垂直于F方向的分速度.第(3)问不能只定性画出轨迹如图2所示,要通过定量计算精确研究轨迹如图2所示.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
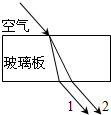 (2012?丰台区一模)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示.下列说法正确的是( )
(2012?丰台区一模)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示.下列说法正确的是( ) (2012?丰台区一模)图中K、L、M为静电场中的3个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依abcde轨迹运动.已知电势?K<?L<?M,且粒子在ab段做减速运动.下列说法中正确的是( )
(2012?丰台区一模)图中K、L、M为静电场中的3个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依abcde轨迹运动.已知电势?K<?L<?M,且粒子在ab段做减速运动.下列说法中正确的是( ) (2012?丰台区一模)一质量M=0.8kg的小物块,用长l=0.8m的细绳悬挂在天花板上,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s2.求:
(2012?丰台区一模)一质量M=0.8kg的小物块,用长l=0.8m的细绳悬挂在天花板上,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s2.求: