题目内容
【题目】如图所示,水平放置的带小孔的金属薄板间有匀强电场,薄板的上极板电势高于下极板,板间距d=1.25m.M恰好在薄板小孔P、N的正上方,距上极板的距离h=1.25m.若从M处由静止释放一个质量m=1×10﹣3kg电荷量为qa=﹣4×10﹣3C的带电小球a,小球a恰好能到达下极板的N孔处而未穿出极板,现若将m=1×10﹣3kg电荷量为qb=﹣5×10﹣3C的带电小球b从M点由静止释放,重力加速度g=10m/s2 , 下列说法正确的是( )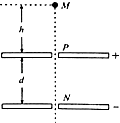
A.薄板间的匀强电场的电场强度为3×105N/C
B.薄板间的匀强电场的电场强度为5×105N/C
C.带电小球a从M处下落至下极板的时间为1.0s
D.带电小球b从M处下落的过程中机械能的变化量为﹣ ![]() J
J
【答案】B,C,D
【解析】解:A、小球由静止开始下落到下端的小球到达下极板的过程中,由动能定理得:
mg(h+d)﹣Eqad=0
解得:E=5×105N/C.故A错误,B正确;
C、对于小球自由下落的过程,有 h= ![]()
解得,t1= ![]() =
= ![]() s=0.5s;
s=0.5s;
小球到达小孔时的速度为 v1= ![]() =
= ![]() m/s=5m/s;
m/s=5m/s;
小球在匀强电场中的加速度 α= ![]()
代入数据得:a=10m/s2;
由0=v﹣at2
代入数据解得:t2=0.5 s.
故带电小球a从M处下落至下极板的时间为:t=t1+t2=0.5s+0.5s=1.0s.故C正确;
D、设带电小球b在电场内下降的高度为x,由动能定理得:mg(h+x)﹣Eqbx=0
代入数据得:x= ![]() m
m
此过程中小球的机械能的改变量等于克服电场力做的功,即△E机=﹣qbEx
代入数据得: ![]() J
J
故选:BCD
对小球由静止开始到下端小球到达下极板的过程中运用动能定理,求出两极板间匀强电场的电场强度.
小球先做自由落体运动,由运动学位移公式求出自由下落到小孔的时间,由位移速度公式求出到达A板小孔的速度.小球在匀强电场中做匀加速运动,根据牛顿第二定律和运动学位移公式结合时间,即可得到总时间.
结合机械能的变化量等于电场力做功,由功能关系求解.