题目内容
17.某质点从静止开始沿直线运动,先做匀加速运动后做匀速运动.运动总时间10s,位移150m.已知质点在加速阶段的第3s内通过的距离为10m,求该质点加速阶段的加速度及在加速阶段通过的距离.分析 因为物体在第3s内的平均速度小于全程的平均速度可知,物体加速运动时间大于3s,根据位移时间关系由第3s内的位移求得物体运动的加速度,再根据位移时间关系求得加速阶段的时间和通过的位移.
解答 解:物体在经3s内的平均速度小于全程的平均速度,故可知,物体加速运动的时间大于3s,故根据位移时间关系由第3s内的位移为10m可得:
$10=\frac{1}{2}a({3}^{3}-{2}^{2})$
由此解得物体加速运动的加速度a=4m/s2
令加速运动的总时间为t,则匀速运动的时间为(10-t)
由物体前10s内运动的位移有:
$\frac{1}{2}a{t}^{2}+(at)(10-t)=150$
代入加速度a=4m/s2解得:t=5s
所以物体加速运动通过的位移x=$\frac{1}{2}×4×{5}^{2}m=50m$
答:该质点加速阶段的加速度为4m/s2,在加速阶段通过的距离为50m.
点评 掌握匀变速直线运动的位移时间关系是正确解题的关键,不难属于基础题.

练习册系列答案
相关题目
7.关于光电效应,下列说法正确的是( )
| A. | 当入射光的频率低于极限频率时,不能发生光电效应 | |
| B. | 光电子的最大初动能与入射光的频率成正比 | |
| C. | 光电子的最大初动能与入射光的强度成正比 | |
| D. | 某单色光照射一金属时不能发生光电效应,改用波长较短的光照射该金属可能发生光电效应 |
6.关于电磁场和电磁波,下列说法正确的是( )
| A. | 把电场和磁场组合在一起就是电磁场 | |
| B. | 无线电波、可见光、Χ射线都是电磁波 | |
| C. | 电磁波频率越高,传播速度越大 | |
| D. | 麦克斯韦第一次通过实验验证了电磁波的存在 |
7. 如图所示,一把塑料尺与毛巾摩擦过程中,有大量电子从塑料尺转移到了毛巾上,那么根据上述信息,说法正确的是( )
如图所示,一把塑料尺与毛巾摩擦过程中,有大量电子从塑料尺转移到了毛巾上,那么根据上述信息,说法正确的是( )
 如图所示,一把塑料尺与毛巾摩擦过程中,有大量电子从塑料尺转移到了毛巾上,那么根据上述信息,说法正确的是( )
如图所示,一把塑料尺与毛巾摩擦过程中,有大量电子从塑料尺转移到了毛巾上,那么根据上述信息,说法正确的是( )| A. | 毛巾呈中性 | B. | 毛巾带正电 | ||
| C. | 毛巾带负电 | D. | 无法判断毛巾是否带电 |
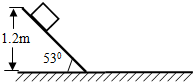 如图所示,固定的斜面与水平面相连接,斜面的倾角为530,一物体从距地面1.2m的斜面顶点由静止滑下.若物体与斜面、地面的动摩擦因数都为0.5,不考虑物体在斜面与地面交接处对物体的影响,求物体在水平地面上滑行的距离.(取sin53°=0.8,cos53°=0.6,g=10m/s2)
如图所示,固定的斜面与水平面相连接,斜面的倾角为530,一物体从距地面1.2m的斜面顶点由静止滑下.若物体与斜面、地面的动摩擦因数都为0.5,不考虑物体在斜面与地面交接处对物体的影响,求物体在水平地面上滑行的距离.(取sin53°=0.8,cos53°=0.6,g=10m/s2) 在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.
在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.
 如图所示,一水平方向的传送带以恒定的速度v=2m/s沿顺时针方向匀速转动,传送带右端固定着一光滑的四分之一圆弧面轨道,并与弧面下端相切.一质量为m=1kg的物体自圆弧面轨道的最高点由静止滑下,圆弧面轨道的半径R=0.45m,物体与传送带之间的动摩擦因数为μ=0.2,不计物体滑过曲面与传送带交接处时的能量损失,传送带足够长,g=10m/s2.求:
如图所示,一水平方向的传送带以恒定的速度v=2m/s沿顺时针方向匀速转动,传送带右端固定着一光滑的四分之一圆弧面轨道,并与弧面下端相切.一质量为m=1kg的物体自圆弧面轨道的最高点由静止滑下,圆弧面轨道的半径R=0.45m,物体与传送带之间的动摩擦因数为μ=0.2,不计物体滑过曲面与传送带交接处时的能量损失,传送带足够长,g=10m/s2.求: