��Ŀ����
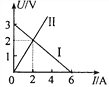
����Ŀ����ij��������ϰ�У�������Ա��һ����ֱ�ij������ɾ�ֹ���£�����2.5s��أ���֪������Ա���֮��Ħ����F�Ĵ�С������������mg�Ĵ�С�ı�ֵ ![]() ��ʱ��ı仯��ͼ��ʾ��gȡ10m/s2 ��
��ʱ��ı仯��ͼ��ʾ��gȡ10m/s2 �� 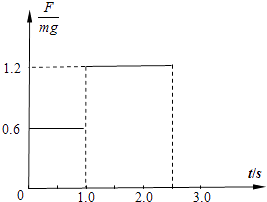
��1����˵��������Ա���»������м��ٶȵĴ�С�ͷ����Ƿ�仯���������Ӧ�ļ��ٶȣ�
��2����������Ա���»�����������ٶȵĴ�С��
��3����������Ա���ʱ�ٶȵĴ�С��
���𰸡�
��1���⣺�ö�Ա����t1=1sʱ���ڣ����ٶȷ������£���С��Ϊa1��
��ţ�ٵڶ����ɵã�mg��F1=ma1
����a1= ![]() =4m/s2
=4m/s2
�ڽ�������t2=1.5sʱ���ڣ����ٶȷ������ϣ���С��Ϊa2��
��ţ�ٵڶ����ɵã�F2��mg=ma2
a2= ![]() =2m/s2
=2m/s2
�ɼ������ٶȵĴ�С�ͷ������˱仯��
�𣺸ö�Ա����t1=1sʱ���ڣ����ٶ�Ϊ4m/s2���������£��ڽ�������t2=1.5sʱ���ڣ����ٶ�Ϊ2m/s2���������ϣ���С�ͷ������ı䣻
��2���⣺�ö�Ա����t1=1sʱ������a1�ȼ����»���Ȼ����t2=1.5sʱ������a2�ȼ����»���
������ٶ�vm=a1t1
�������ݽ�ã�vm=4m/s
��������Ա���»�����������ٶȵĴ�СΪ4m/s��
��3���⣺��Ա���ʱ���ٶ�v=vm��a2t2
�������ݽ�ã�v=1m/s
��������Ա���ʱ�ٶȵĴ�СΪ1m/s��
������������ͼ��������ӵ�������������Ա������֮�ȣ�����������Ա���˶����������ţ�ٵڶ�����������ٶȣ����ٶȹ�ʽ�������ٶȺ���ص��ٶȣ�
�����㾫�����������⣬������Ҫ�˽�ţ�ٶ�����ͼ��(ţ�ٵڶ����ɶ�����ʾ�������˶��Ĺ�ϵ����֪���������ɸ���ţ�ٵڶ����ɣ�������������˶����ɣ���ţ�ٵڶ����ɵ���ѧ����ʽF��=ma��F��������ma����������Ч�����ر�Ҫע�ⲻ�ܰ�ma��������)��

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�