题目内容
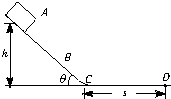
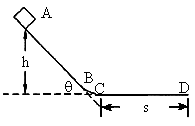
图中ABCD是一条长轨道,其中AB段是倾斜角为θ的斜面,CD段是水平的.BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止状态释放.沿轨道滑下,最后停在D点,A点和D点的位置如图所示.现用一沿着轨道方向的力推滑块。把它缓慢地由D点推回到A点时停下.设滑块与轨道间的动摩擦因数为μ则推力对滑块做的功等于
[ ]
A.mgh
B.2mgh
C.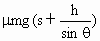
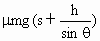
D.μmgs+μmghcotθ
答案:B
解析:
解析:
|
小滑块在斜面上和在平面上运动时都受到三个力.即重力、支持力和摩擦力.整个过程中,支持力由于与速度方向始终垂直,故不做功.从 A到D的过程中,由动能定理,有
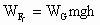 . .
当它返回时,从 D到A的过程中,重力和摩擦力均做负功,因推力平行于轨道,所受摩擦力大小跟A到D过程相同,做的功也相等,均为-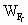 .从D到A的返回过程.根据动能定理,有 .从D到A的返回过程.根据动能定理,有
本题中,往返两过程均克服摩擦力做功,且相等,所以不必通过求力和位移找摩擦力做功的表达式. |

练习册系列答案
相关题目
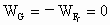
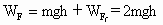
 图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点推回到A点,设滑块与轨道间的动摩擦系数为μ,则推力对滑块做的功等于( )
图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点推回到A点,设滑块与轨道间的动摩擦系数为μ,则推力对滑块做的功等于( )
 ) D.μmgs+μmgshcosθ
) D.μmgs+μmgshcosθ

 B.
B.
 D.
D.