题目内容
5.物体做自由落体运动,Ek代表动能,Ep代表势能,h代表下落的距离,以水平地面为零势能面.下列所示图象中,能正确反映各物理量之间关系的是( )| A. | 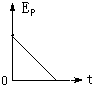 | B. | 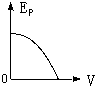 | C. | 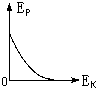 | D. | 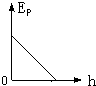 |
分析 根据运动学公式以及机械能守恒分别求出EK与t、v、EP和h的关系式,判断关系图线是否正确.
解答 解:自由落体运动的速度v=gt,动能Ek=12mv2=12mg2t2,EK与t成二次函数关系.
物体的重力势能:EP=E−Ek=E−12mg2t2,EP与t成二次函数关系,开口的方向向下.故A错误.
B、根据Ek=12mv2知,EK与v成二次函数关系;物体的重力势能:EP=E−Ek=E−12mv2,EP与t成二次函数关系,开口的方向向下.故B正确.
C、因为在整个运动的过程中,机械能守恒,所以EK+EP=C(常量),所以EK=C-EP,EK与EP成一次函数关系.故C错误.
D、根据重力势能的表达式得,EP=mgH=mg(H0-h),知EK与h成线性关系.故D正确.
故选:BD.
点评 解决本题的关键能够熟练运用动能定理、机械能守恒定律以及运动学公式,得出关系式进行判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.一定质量的理想气体经过如图所示的变化过程,下列说法正确的是( )
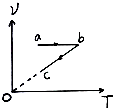

| A. | ab过程中,气体的压强减小 | |
| B. | ab过程中,气体分子的平均动能增大 | |
| C. | bc过程中,气体对外做功,温度降低 | |
| D. | bc过程中,气体的密度增大 |
20.下列几种情况下力F都对物体做了功:
①水平推力F推着质量为m的物体从静止开始在光滑水平面上前进了S;
②水平推力F推着质量为m的物体从静止开始在粗糙水平面上前进了S.
下列关于力F所做的功说法正确的是( )
①水平推力F推着质量为m的物体从静止开始在光滑水平面上前进了S;
②水平推力F推着质量为m的物体从静止开始在粗糙水平面上前进了S.
下列关于力F所做的功说法正确的是( )
| A. | ①做功最多 | B. | ②做功最多 | C. | 无法确定 | D. | 做功都相等 |
17.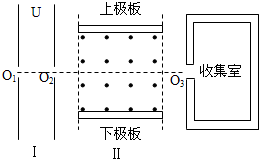 如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
 如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )| A. | 区域Ⅱ的电场方向竖直向下 | |
| B. | 该装置可筛选出具有特定质量的粒子 | |
| C. | 该装置可筛选出具有特定速度的粒子 | |
| D. | 若射入的粒子电荷量相同,则该装置筛选出的粒子一定具有相同的质量 |
15. 如图所示,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R,开始时,开关断开.当开关接通时,以下说法正确的是( )
如图所示,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R,开始时,开关断开.当开关接通时,以下说法正确的是( )
 如图所示,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R,开始时,开关断开.当开关接通时,以下说法正确的是( )
如图所示,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R,开始时,开关断开.当开关接通时,以下说法正确的是( )| A. | 副线圈两端MN输出电压增大 | B. | 通过灯泡L1的电流减小 | ||
| C. | 电流表的示数减小 | D. | 变压器的输入功率变小 |
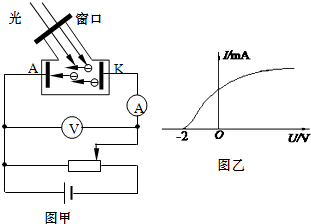
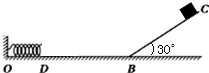 如图所示,水平轨道ODB与一斜面BC平滑相交于B点,斜面BC与水平面的夹角为30°,水平轨道OD段光滑,DB段粗糙,DB段长度L=2m,动摩擦因数?=0.1,BC段光滑且长度S=3.6m,轻质弹簧左端固定于O点,弹簧原长时,右端恰好处于D点.现把质量m=2kg的可视为质点的小滑块由C点静止释放,沿CB下滑,进入水平轨道继续滑行后压缩弹簧,设滑块在经过B点瞬间速率大小不变(取g=10m/s2,空气阻力不计).
如图所示,水平轨道ODB与一斜面BC平滑相交于B点,斜面BC与水平面的夹角为30°,水平轨道OD段光滑,DB段粗糙,DB段长度L=2m,动摩擦因数?=0.1,BC段光滑且长度S=3.6m,轻质弹簧左端固定于O点,弹簧原长时,右端恰好处于D点.现把质量m=2kg的可视为质点的小滑块由C点静止释放,沿CB下滑,进入水平轨道继续滑行后压缩弹簧,设滑块在经过B点瞬间速率大小不变(取g=10m/s2,空气阻力不计). 如图,一上端开口,下端封闭的细长玻璃管,下部有长l1=66cm的水银柱,中间封有长l2=6.5cm的空气柱,上部有长l3=56cm的水银柱,此时水银面恰好与管口平齐.已知大气压强为p0=76cmHg.如果使玻璃管绕底端在竖直平面内缓慢地转动一周,求在开口向下和转回到原来位置时管中空气柱的长度.封入的气体可视为理想气体,在转动过程中没有发生漏气.
如图,一上端开口,下端封闭的细长玻璃管,下部有长l1=66cm的水银柱,中间封有长l2=6.5cm的空气柱,上部有长l3=56cm的水银柱,此时水银面恰好与管口平齐.已知大气压强为p0=76cmHg.如果使玻璃管绕底端在竖直平面内缓慢地转动一周,求在开口向下和转回到原来位置时管中空气柱的长度.封入的气体可视为理想气体,在转动过程中没有发生漏气.