题目内容
 (1)2006年美国和俄罗斯的科学家利用回旋加速器,通过(钙48)轰击(锎249)发生核反应,成功合成了第1 18号元素,这是迄今为止门捷列夫元素周期表中原子序数最大的元素,实验表明,该元素的原子核先放出3个相同的粒子x,再连续经过3次α衰变后,变成质量数为282的第112号元素的原子核,则上述过程中的粒子x是
(1)2006年美国和俄罗斯的科学家利用回旋加速器,通过(钙48)轰击(锎249)发生核反应,成功合成了第1 18号元素,这是迄今为止门捷列夫元素周期表中原子序数最大的元素,实验表明,该元素的原子核先放出3个相同的粒子x,再连续经过3次α衰变后,变成质量数为282的第112号元素的原子核,则上述过程中的粒子x是A.中子 B质子 C.电子 D.α粒子
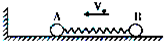
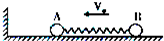
(2)如图所示,质量为6kg的小球A与质量为3kg的小球B,用轻弹簧相连后在光滑的水平面上以速度v0向左匀速运动,在A球与左侧墙壁碰,撞后两球继续运动的过程中,弹簧的最大弹性势能为4J,若A球与左墙壁碰撞前后无机械能损失,试求v0的大小:
分析:(1)根据电荷数守恒,配平核反应方程式,确定粒子x.
(2)A球与左墙壁碰撞前后无机械能损失,以原速率反弹,当两球的速度相同时,弹簧的弹性势能最大,根据系统的动量守恒和机械能守恒结合求解v0的大小:
(2)A球与左墙壁碰撞前后无机械能损失,以原速率反弹,当两球的速度相同时,弹簧的弹性势能最大,根据系统的动量守恒和机械能守恒结合求解v0的大小:
解答:解:(1)第118号元素的电荷数为118,第112号元素的电荷数是112,则根据电荷数守恒得粒子x是:118-3×2-112=0.故该粒子x是中子.故选A
(2)由于A球与左墙壁碰撞前后无机械能损失,所以A球与左侧墙壁碰撞后的速度大小仍为v0,方向水平向右.由题意分析可知,在A球与墙壁碰撞后继续运动的过程中,当两球的速度相同时,弹簧的弹性势能最大,根据系统的动量守恒和机械能守恒,得:
mAv0-mBv0=(mA+mB)v
(mA+mB)
=
(mA+mB)v2+Ep
联立解得:v0=
=1m/s
故答案为:(1)A;(2)v0的大小是1m/s.
(2)由于A球与左墙壁碰撞前后无机械能损失,所以A球与左侧墙壁碰撞后的速度大小仍为v0,方向水平向右.由题意分析可知,在A球与墙壁碰撞后继续运动的过程中,当两球的速度相同时,弹簧的弹性势能最大,根据系统的动量守恒和机械能守恒,得:
mAv0-mBv0=(mA+mB)v
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
联立解得:v0=
|
故答案为:(1)A;(2)v0的大小是1m/s.
点评:对于核反应方程,根据质量数守恒和电荷数守恒进行配平,可确定x是何粒子.对于含有弹簧的系统,往往根据动量守恒和机械能守恒进行研究,关键要抓住弹簧弹性势能最大时两球的速度相同这个条件.

练习册系列答案
相关题目