题目内容
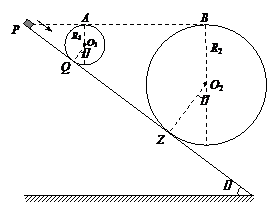
如下图1是过山车的实物图,图2为过山车的模型图.在模型图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道固定在倾角为α=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点高度相同,圆形轨道与斜轨道之间连接圆滑.为使小车从P点以一定的初速度沿斜面向下运动能过A、B两点,求小车在P点的速度应满足什么条件?(小车可视作质点,已知斜轨道面与小车间的动摩擦因数为μ=
.g取10m/s2,sin37°=0.6,cos37°=0.8)
| 1 | 24 |

分析:首先根据小车在P点的初速度10m/s,与第一问中v0比较,分析小车能否安全通过圆弧轨道O1.若小车恰能通过B点,由重力提供向心力,由牛顿第二定律列方程,求出小车通过B点的临界速度,根据动能定理求出小车在P点的临界速度,再确定小车能否安全通过两个圆形轨道.
解答:解:由动能定理可得小车在B点的速度小于在A点的速度,而过最高点的临界速度满足 mg=
,故小车若能过B点,则一定能过A点.
设小车在P点的速度为v0时,恰能过B点,则在B点时有:mg=
.
P点到B点的过程,由动能定理得:-(μmgcosα)L2=
mv
-
mv
其中L2为PZ的距离,满足L2=
=24m/s
解得:v0=4
m/s
则小车在P点的速度满足的条件为vp≥4
m/s.
答:小车在P点的速度应满足的条件是vp≥4
m/s.
| mv2 |
| R |
设小车在P点的速度为v0时,恰能过B点,则在B点时有:mg=
m
| ||
| R2 |
P点到B点的过程,由动能定理得:-(μmgcosα)L2=
| 1 |
| 2 |
2 B |
| 1 |
| 2 |
2 0 |
其中L2为PZ的距离,满足L2=
| R2(1+cosα) |
| sinα |
解得:v0=4
| 6 |
则小车在P点的速度满足的条件为vp≥4
| 6 |
答:小车在P点的速度应满足的条件是vp≥4
| 6 |
点评:本题是竖直平面内圆周运动的类型,关键抓住最高点的临界条件,结合动能定理分析求解.

练习册系列答案
相关题目



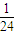 .g取10m/s2,sin37°=0.6,cos37°=0.8)
.g取10m/s2,sin37°=0.6,cos37°=0.8)