��Ŀ����
6��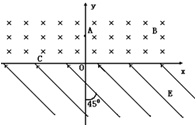 ��ͼʾ�����У�X���Ϸ���һ��ǿ�ų����Ÿ�Ӧǿ�ȵķ���ֱֽ�������СΪB������һ�������ٶ�v0��Y���ϵ�A����Y������������ų��������ڴų����˶�һ��ʱ���Ժ��C�����X���·�����ǿ�糡�����У���C���ٶȷ�����X��������н�Ϊ45�㣬����ǿ�糡��ǿ�ȴ�СΪE��������Y��н�Ϊ45����б�����Ϸ�����֪���ӵ�����Ϊm������Ϊq���������ӵ����������ų�����͵糡�����㹻����
��ͼʾ�����У�X���Ϸ���һ��ǿ�ų����Ÿ�Ӧǿ�ȵķ���ֱֽ�������СΪB������һ�������ٶ�v0��Y���ϵ�A����Y������������ų��������ڴų����˶�һ��ʱ���Ժ��C�����X���·�����ǿ�糡�����У���C���ٶȷ�����X��������н�Ϊ45�㣬����ǿ�糡��ǿ�ȴ�СΪE��������Y��н�Ϊ45����б�����Ϸ�����֪���ӵ�����Ϊm������Ϊq���������ӵ����������ų�����͵糡�����㹻������1��C������꣮
��2�����Ӵ�A������������δ�ԽX��ʱ���˶�ʱ�䣮
��3�����ӵ��Ĵδ�ԽX��ʱ�ٶȵĴ�С���ٶȷ�����糡E����ļнǵ�����ֵ��
���� ��1�����������ڴų���������Բ���˶��������������䵱�����������Բ�İ뾶�����ɼ��ι�ϵ�ɵó�C������ꣻ
��2���������ӵ����ξ���x��ʱ���˶����̣��ɼ��ι�ϵ��֪�������ڴų���ת���ĽǶȣ��Ӷ�����侭����ʱ�䣬�ڵ糡����������ƽ���˶������ٶȵĺϳ���ֽ��ϵ����õ糡�е�ʱ�䣬�Ӷ������ʱ�䣻
��3�������ڴų���������Բ���˶�����һ�ν���ų�ʱ�������˶����ٽ���ų�����Բ���˶����˺����糡����ƽ���˶����ɼ��ι�ϵ���˶��ĺϳ���ֽ����ý����
��� �⣺��1�����������ڴų���������Բ���˶������������䵱�����������У�
$q{v_0}B=\frac{mv_0^2}{R}$
R=$\frac{m{v}_{0}}{Bq}$��
�ɼ��ι�ϵ��֪��
xC=-��R+Rcos45�㣩=-$\frac{m{v}_{0}}{Bq}$��1+$\frac{\sqrt{2}}{2}$�� �ã�C����Ϊ����-$\frac{2+\sqrt{2}}{2}\frac{m{v}_{0}}{Bq}$��0��
�ã�C����Ϊ����-$\frac{2+\sqrt{2}}{2}\frac{m{v}_{0}}{Bq}$��0��
��2�����������ڽ���糡���������˶�����ԭ���أ�Ȼ���ٽ���ų�����Բ���˶�����ʱ������ų��е�ʱ�估�糡��������ʱ�䣻���У�
�ڴų���$T=\frac{2��R}{v_0}$
$T=\frac{2��m}{qB}$
${t_��}=\frac{{\frac{7}{4}��}}{2��}T=\frac{7��m}{4qB}$��
�ڵ糡��Eq=ma
${t_��}=\frac{{2{v_0}}}{a}=\frac{{2m{v_0}}}{qE}$
$t={t_��}+{t_��}=\frac{{2m{v_0}}}{qE}+\frac{7��m}{4qB}$��
��3�����ӵ����δ�Խx����ڵ糡������ƽ���˶�������v0��x�������45���ǣ����Ե��Ĵδ�Խx��ʱ��
${v}_{0}{t}_{4}=\frac{1}{2}\frac{qE}{m}•{t}_{4}^{2}$
�ã�${t}_{4}=\frac{2m{v}_{0}}{qE}$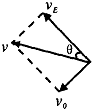 �ص糡�����ٶȵķ���Ϊ��${v}_{E}=\frac{qE}{m}•{t}_{4}=2{v}_{0}$
�ص糡�����ٶȵķ���Ϊ��${v}_{E}=\frac{qE}{m}•{t}_{4}=2{v}_{0}$
���ԣ��ٶȵĴ�СΪ$v=\sqrt{{v}_{0}^{2}+{v}_{E}^{2}}=\sqrt{5}{v}_{0}$
�ٶȷ�����糡E�ļн���Ϊ�ȣ���ͼ��ʾ����$tan��=\frac{{v}_{0}}{{v}_{E}}=\frac{1}{2}$
�ã�$��=arctan\frac{1}{2}$
�𣺣�1��C�������Ϊ��-$\frac{2+\sqrt{2}}{2}\frac{m{v}_{0}}{Bq}$��0����
��2�����Ӵ�A������������δ�ԽX��ʱ���˶�ʱ����$\frac{2m{v}_{0}}{qE}+\frac{7��m}{4qB}$��
��3�����ӵ��Ĵδ�ԽX��ʱ�ٶȵĴ�С��$\sqrt{5}{v}_{0}$���ٶȷ�����糡E����ļнǵ�����ֵ��$\frac{1}{2}$��
���� ������̺ܸ��ӣ�Ҫע����������������ӵ��˶�������ֱ����õ糡���ų��е����ʽ��з����˶���Ҫע�⼸�ι�ϵ����ȷӦ�ã�

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д� Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д�X+${\;}_{3}^{7}$Li��2Y
Y+${\;}_{4}^{14}$N��X+${\;}_{8}^{17}$O
Y+${\;}_{4}^{9}$Be��Z+${\;}_{6}^{12}$C
X��Y��Z�����ֲ�ͬ�����ӣ�����Z�ǣ�������
| A�� | ������ | B�� | ���� | C�� | ���� | D�� | ���� |

| A�� | 2.5 sǰС����������˶� | B�� | 2.5 s��С����������˶� | ||
| C�� | 2.5 sǰС������Ħ�������� | D�� | 2.5 s��С������Ħ�������� |
 ��ͼ��ʾ��һ����ΪM��ľ����ˮƽ��Ӵ���ľ���Ϸ��̶���һ��ֱ���ľ�Ե�ᵯ�ɣ����϶�ϵһ����������Ϊm��С���ɲ����磩��С������ֱ����������������ֱ�������ǿ�糡���ڵ������ûָ���ԭ��ʱ��С���������ٶȣ���ľ���ˮƽ��ѹ��Ϊ��ʱ��С��ļ��ٶȴ�С�ǣ�������
��ͼ��ʾ��һ����ΪM��ľ����ˮƽ��Ӵ���ľ���Ϸ��̶���һ��ֱ���ľ�Ե�ᵯ�ɣ����϶�ϵһ����������Ϊm��С���ɲ����磩��С������ֱ����������������ֱ�������ǿ�糡���ڵ������ûָ���ԭ��ʱ��С���������ٶȣ���ľ���ˮƽ��ѹ��Ϊ��ʱ��С��ļ��ٶȴ�С�ǣ�������| A�� | $\frac{mg}{M}$ | B�� | $\frac{��M+m��g}{m}$ | C�� | $\frac{Mg}{m}$ | D�� | $\frac{��M+m��g}{M}$ |
 ﮵���������ߡ�����������Ⱦ���㷺ʹ�����ֻ��ȵ��Ӳ�Ʒ�У����ó����Ϊһ�ֻ�﮵�س�磬��Ч��·��ͼ��ʾ���������Դ�������ѹΪU���������ΪI���ֻ���ص�����Ϊr������˵����ȷ���ǣ�������
﮵���������ߡ�����������Ⱦ���㷺ʹ�����ֻ��ȵ��Ӳ�Ʒ�У����ó����Ϊһ�ֻ�﮵�س�磬��Ч��·��ͼ��ʾ���������Դ�������ѹΪU���������ΪI���ֻ���ص�����Ϊr������˵����ȷ���ǣ�������| A�� | ����ת��Ϊ��ѧ�ܵĹ���ΪUI | B�� | ���������ĵ繦��ΪUI | ||
| C�� | ��ز������ȹ���ΪI2r | D�� | ������ij��Ч��Ϊ$\frac{Ir}{U}$��100% |
 ��ͼ��ʾ��һ�ܳ��ġ������쳤��������������⻬�����֣������˸�ϵһС��a��b��a������Ϊm�������ڵ��棻b������Ϊ4m��������ס���߶�Ϊh����ʱ�����պ��������Ӿ�ֹ��ʼ�ͷ�b��a�����������߶�Ϊ��������
��ͼ��ʾ��һ�ܳ��ġ������쳤��������������⻬�����֣������˸�ϵһС��a��b��a������Ϊm�������ڵ��棻b������Ϊ4m��������ס���߶�Ϊh����ʱ�����պ��������Ӿ�ֹ��ʼ�ͷ�b��a�����������߶�Ϊ��������| A�� | h | B�� | 1.5h | C�� | 1.6h | D�� | 2.2h |
| A�� | Ϊ�˱������ص�ˮ�֣����Գ��ɵ��棬�ƻ��������ëϸ�� | |
| B�� | ����dz�㺣ˮ����㺣ˮ֮����¶Ȳ�����һ���Ȼ�������ˮ��һ��������ת��Ϊ��е���ǿ��ܵ� | |
| C�� | ����������������������ܱض����� | |
| D�� | Һ���Ĺ�ѧ���ʲ����¶ȡ�������ñ仯���ı� | |
| E�� | �����Ǿ��廹�ǷǾ��壬�ȽϿɿ��İ취�Ǵ��ۻ������¶��Ƿ�仯���жϣ� |