题目内容
(2012?湖南一模)如图a所示,一个质量为m=2.0×10-11kg,电荷量q=1.0×10-5C的带负电粒子(重力忽略不计),从静止开始经U1=100V电压加速后,垂直于场强方向进入两平行金属板间的匀强偏转电场.偏转电场的电压U2=100V,金属板长L=20cm,两板间距d=1O
cm.
(1)粒子进人偏转电场时的速度v0大小;

(2)粒子射出偏转电场时的偏转角θ;
(3)在匀强电场的右边有一个足够大的匀强磁场区域.若以粒子进入磁场的时刻为t=0,磁感应强度B的大小和方向随时间的变化如图b所示,图中以磁场垂直于纸面向内为正,建立如图直角坐标系(坐标原点为微粒进入偏转电场时初速度方向与磁场的交边界点).求在t=
×10-6s时粒子的位置坐标(X,Y).(答案可以用根式表示,如用小数,请保留两位有效数字)
| 3 |
(1)粒子进人偏转电场时的速度v0大小;

(2)粒子射出偏转电场时的偏转角θ;
(3)在匀强电场的右边有一个足够大的匀强磁场区域.若以粒子进入磁场的时刻为t=0,磁感应强度B的大小和方向随时间的变化如图b所示,图中以磁场垂直于纸面向内为正,建立如图直角坐标系(坐标原点为微粒进入偏转电场时初速度方向与磁场的交边界点).求在t=
| 4π |
| 3 |
分析:(1)对于粒子在加速电场中运动过程,根据动能定理求解速度v0大小;
(2)粒子在偏转电场中做类平抛运动,运用运动的分解,根据牛顿第二定律和运动学公式求解偏转角θ;
(3)粒子进入磁场后,则洛伦兹力提供向心力做匀速圆周运动,由牛顿第二定律和圆周运动的公式求出周期,由t=
T分析所给的时间内,轨迹对应的圆心角,画出轨迹,由几何知识求出坐标.
(2)粒子在偏转电场中做类平抛运动,运用运动的分解,根据牛顿第二定律和运动学公式求解偏转角θ;
(3)粒子进入磁场后,则洛伦兹力提供向心力做匀速圆周运动,由牛顿第二定律和圆周运动的公式求出周期,由t=
| θ |
| 2π |
解答:解:(1)粒子在加速电场中,由动能定理得
qU1=
m
解得v0=1.0×104m/s
(2)粒子在偏转电场中做类平抛运动,有 a=
,
vy=at=a
飞出电场时,速度偏转角的正切:tanθ=
=
=
解得 θ=30°
(3)进入磁场时粒子的速度为 v=
=
×104m/s
飞出电场时,偏转距离y=
at2=
=
m=
m
设粒子在磁场中做圆周运动的周期为T,半径为r,则由
qvB=m
得 r=
=
×10-2s
T=
=
=2π×10-6s
依题意,在t=0到t=
×10-6s内和
×10-6s到
×10-6s时间内在磁场中转过的圆弧所对的圆心角均为
,粒子的运动轨迹如图所示,
由几何关系得X=2(r+rsin30°)=2
×10-2m≈3.5×10-2m
Y=y-2rcos30°=(
-
)m≈3.8×10-2m
答:(1)粒子进人偏转电场时的速度v0大小是1.0×104m/s;
(2)粒子射出偏转电场时的偏转角θ是30°;
(3)在t=
×10-6s时粒子的位置坐标为(3.5×10-2m,3.8×10-2m).

qU1=
| 1 |
| 2 |
| v | 2 0 |
解得v0=1.0×104m/s
(2)粒子在偏转电场中做类平抛运动,有 a=
| qU2 |
| md |
vy=at=a
| L |
| v0 |
飞出电场时,速度偏转角的正切:tanθ=
| vy |
| v0 |
| U2L |
| 2U1d |
| 1 | ||
|
解得 θ=30°
(3)进入磁场时粒子的速度为 v=
| v0 |
| cosθ |
2
| ||
| 3 |
飞出电场时,偏转距离y=
| 1 |
| 2 |
| U2L2 |
| 4U1d |
| 1 | ||
10
|
| ||
| 30 |
设粒子在磁场中做圆周运动的周期为T,半径为r,则由
qvB=m
| v2 |
| r |
得 r=
| mv |
| qB |
2
| ||
| 3 |
T=
| 2πr |
| v |
| 2πm |
| qB |
依题意,在t=0到t=
| 2π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
| 2π |
| 3 |
由几何关系得X=2(r+rsin30°)=2
| 3 |
Y=y-2rcos30°=(
| ||
| 30 |
| 1 |
| 50 |
答:(1)粒子进人偏转电场时的速度v0大小是1.0×104m/s;
(2)粒子射出偏转电场时的偏转角θ是30°;
(3)在t=
| 4π |
| 3 |
点评:本题中带电粒子在组成场中运动,要掌握三种场中的研究方法,难点是粒子在磁场中的运动,根据时间与周期的关系,确定圆心角,由几何知识求解坐标.

练习册系列答案
相关题目
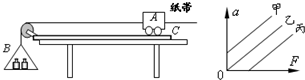 (2012?湖南一模)如图所示为“探究加速度与物体受力与质量的关系”实验装置图.图中A为小车,B为装有砝码的小桶,C为一端带有定滑轮的长木板,小车通过纸带与电火花打点计时器相连,计时器接50HZ交流电.小车的质量为m1,小桶(及砝码)的质量为m2.
(2012?湖南一模)如图所示为“探究加速度与物体受力与质量的关系”实验装置图.图中A为小车,B为装有砝码的小桶,C为一端带有定滑轮的长木板,小车通过纸带与电火花打点计时器相连,计时器接50HZ交流电.小车的质量为m1,小桶(及砝码)的质量为m2. (2012?湖南一模)如图所示,在高为h=5m的平台右边缘上,放着一个质量M=3kg的铁块,现有一质量为m=1kg的钢球以v0=10m/s的水平速度与铁块在极短的时间内发生正碰被反弹,落地点距离平台右边缘的水平距离为l=2m.已知铁块与平台之间的动摩擦因数为0.5,求铁块在平台上滑行的距离s(不计空气阻力,铁块和钢球都看成质点).
(2012?湖南一模)如图所示,在高为h=5m的平台右边缘上,放着一个质量M=3kg的铁块,现有一质量为m=1kg的钢球以v0=10m/s的水平速度与铁块在极短的时间内发生正碰被反弹,落地点距离平台右边缘的水平距离为l=2m.已知铁块与平台之间的动摩擦因数为0.5,求铁块在平台上滑行的距离s(不计空气阻力,铁块和钢球都看成质点). (2012?湖南一模)某同学为了测电流表A1的内阻r1的精确值,准备了如下器材:
(2012?湖南一模)某同学为了测电流表A1的内阻r1的精确值,准备了如下器材: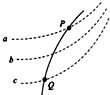 (2012?湖南一模)如图,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,质点从Q到P过程下列说法正确的是( )
(2012?湖南一模)如图,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,质点从Q到P过程下列说法正确的是( )