题目内容
(1)在用插针法测定玻璃砖折射率的实验中,某同学由于没有量角器,他在完成了光路图以后,以O点为圆心、10.00cm长为半径画圆,分别交线段OA于A点,交O、O′连线延长线于C点.过A点作法线NN′的垂线AB交NN′于B点,过C点作法线NN′的垂线CD交NN′于D点,如图1所示.用刻度尺量得OB=8.00cm,CD=4.00cm.由此可得出玻璃折射率n= .
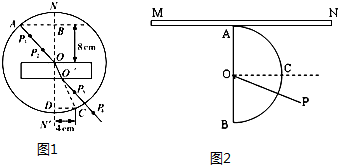
(2)小明同学设计了一个用刻度尺测半圆形玻璃砖折射率的实验(如图2所示),他进行的主要步骤是:
A.用刻度尺测玻璃砖的直径AB的大小d.
B.先把白纸固定在木板上,将玻璃砖水平放置在白纸上,用笔描出玻璃砖的边界,将玻璃砖移走,标出玻璃砖的圆心O、直径AB、AB的法线OC.
C.将玻璃砖放回白纸的原处,长直尺MN紧靠A点并与直径AB垂直放置.
D.调节激光器,使PO光线从玻璃砖圆弧面沿半径方向射向圆心O,并使长直尺MN的左右两端均出现亮点,记下左侧亮点到A点的距离x1,右侧亮点到A点的距离x2.则
①小明利用实验数据计算玻璃折射率的表达式n= .
②关于上述实验以下说法正确的是 .
A.在∠BOC的范围内,改变入射光PO的入射角,直尺MN上可能只出现一个亮点
B.左侧亮点到A点的距离x1一定小于右侧亮点到A点的距离x2
C.左侧亮点到A点的距离x1一定大于右侧亮点到A点的距离x2
D.要使左侧亮点到A点的距离x1增大,应减小入射角.

(2)小明同学设计了一个用刻度尺测半圆形玻璃砖折射率的实验(如图2所示),他进行的主要步骤是:
A.用刻度尺测玻璃砖的直径AB的大小d.
B.先把白纸固定在木板上,将玻璃砖水平放置在白纸上,用笔描出玻璃砖的边界,将玻璃砖移走,标出玻璃砖的圆心O、直径AB、AB的法线OC.
C.将玻璃砖放回白纸的原处,长直尺MN紧靠A点并与直径AB垂直放置.
D.调节激光器,使PO光线从玻璃砖圆弧面沿半径方向射向圆心O,并使长直尺MN的左右两端均出现亮点,记下左侧亮点到A点的距离x1,右侧亮点到A点的距离x2.则
①小明利用实验数据计算玻璃折射率的表达式n=
②关于上述实验以下说法正确的是
A.在∠BOC的范围内,改变入射光PO的入射角,直尺MN上可能只出现一个亮点
B.左侧亮点到A点的距离x1一定小于右侧亮点到A点的距离x2
C.左侧亮点到A点的距离x1一定大于右侧亮点到A点的距离x2
D.要使左侧亮点到A点的距离x1增大,应减小入射角.
分析:(1)根据几何知识求出入射角和折射角的正弦值,再根据折射率定义公式列式求解即可;
(2)PO光线在AB面上发生折射和反射,结合几何关系和折射定律求出折射率的表达式.当∠BOC大于一定角度,将会发生全反射,不会发生折射,结合几何关系,比较x1和x2的大小.
(2)PO光线在AB面上发生折射和反射,结合几何关系和折射定律求出折射率的表达式.当∠BOC大于一定角度,将会发生全反射,不会发生折射,结合几何关系,比较x1和x2的大小.
解答:解:(1)图中P1P2作为入射光线,OO′是折射光线,设光线在玻璃砖上表面的入射角为i,折射角为r,则由几何知识得到:
sini=
,sinr=
又AO=OC,则得折射率 n=
=
=
=1.5.
(2)①设光线在AB面上的入射角为α,折射角为β,
根据几何关系有:sinα=
,sinβ=
.
则折射率n=
=
.
②A、在∠BOC大于等于全发射的临界角,只有反射没有折射,则直尺MN上只出现一个亮点.故A正确.
B、光从玻璃射入真空,折射角大于入射角,通过几何关系知,x1<x2,故B正确,C错误.
D、减小入射角,则折射角较小,x1增大.故D正确.
故选:ABD.
故答案为:
(1)1.5 (2)①
. ②ABD
sini=
| AB |
| AO |
| CD |
| OC |
又AO=OC,则得折射率 n=
| sini |
| sinr |
| AB |
| CD |
| ||
| 4 |
(2)①设光线在AB面上的入射角为α,折射角为β,
根据几何关系有:sinα=
| ||||||
|
| ||||||
|
则折射率n=
| sinβ |
| sinα |
|
②A、在∠BOC大于等于全发射的临界角,只有反射没有折射,则直尺MN上只出现一个亮点.故A正确.
B、光从玻璃射入真空,折射角大于入射角,通过几何关系知,x1<x2,故B正确,C错误.
D、减小入射角,则折射角较小,x1增大.故D正确.
故选:ABD.
故答案为:
(1)1.5 (2)①
|
点评:本题是插针法测定玻璃砖的折射率,实验原理是折射定律,采用单位圆法处理数据,根据原理分析实验误差.

练习册系列答案
相关题目
 (1)在用插针法测定玻璃砖折射率的实验中,甲、乙、丙三位同学在纸上画出的界面aa′、bb′与玻璃砖位置的关系分别如图①、②和③所示,其中甲、丙两同学用的是矩形玻璃砖,乙同学用的是
(1)在用插针法测定玻璃砖折射率的实验中,甲、乙、丙三位同学在纸上画出的界面aa′、bb′与玻璃砖位置的关系分别如图①、②和③所示,其中甲、丙两同学用的是矩形玻璃砖,乙同学用的是