题目内容
11.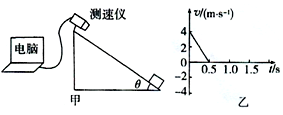 某同学为了测定木块与斜面间的动摩擦因数,他用测速仪研究木块在斜面上的运动情况,装置如图甲所示.他使木块以4m/s的初速度沿倾角30°的斜面上滑紧接着下滑至出发点,并同时开始记录数据,结果电脑只绘出了木块从开始上滑至最高点的v-t图线如图乙所示.g取10m/s2.求:
某同学为了测定木块与斜面间的动摩擦因数,他用测速仪研究木块在斜面上的运动情况,装置如图甲所示.他使木块以4m/s的初速度沿倾角30°的斜面上滑紧接着下滑至出发点,并同时开始记录数据,结果电脑只绘出了木块从开始上滑至最高点的v-t图线如图乙所示.g取10m/s2.求:(1)木块与斜面间的动摩擦因数μ;
(2)木块回到出发点时的速度大小v.
分析 (1)由v-t图象可以求出上滑过程的加速度.由牛顿第二定律可以得到摩擦因数.
(2)由运动学可得上滑距离,上下距离相等,由牛顿第二定律可得下滑的加速度,再由运动学可得下滑至出发点的速度.
解答 解:(1)由题图乙可知,木块经0.5s滑至最高点,由加速度定义式a=$\frac{△v}{△t}$ 有:
上滑过程中加速度的大小:
a1=$\frac{{v}_{0}}{△{t}_{1}}$=$\frac{4}{0.5}$m/s2=8m/s2
上滑过程中沿斜面向下受重力的分力,摩擦力,由牛顿第二定律F=ma得上滑过程中有:
mgsinθ+μmgcosθ=ma1
代入数据得:μ=0.35.
(2)下滑的距离等于上滑的距离:
x=$\frac{{v}_{0}^{2}}{2{a}_{1}}$=$\frac{{4}^{2}}{2×8}$m=1m
下滑摩擦力方向变为向上,由牛顿第二定律F=ma得:
下滑过程中:mgsinθ-μmgcosθ=ma2
解得:a2=gsinθ-μgcosθ=10×$\frac{1}{2}$-0.35×10×$\frac{\sqrt{3}}{2}$=2m/s2
下滑至出发点的速度大小为:v=$\sqrt{2{a}_{2}x}$
联立解得:v=2m/s
答:(1)木块与斜面间的动摩擦因数0.35;
(2)木块回到出发点时的速度大小2m/s.
点评 解决本题的关键能够正确地受力分析,运用牛顿第二定律和运动学公式联合求解,注意掌握图象信息的确定是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.质点做直线运动的位移x与时间t的关系为x=8t+8t2(各物理量均采用国际单位制单位),则该质点( )
| A. | 第2s内的位移是10m | B. | 前2s内的平均速度是24m/s | ||
| C. | 任意相邻2s内的位移差都是8m | D. | 任意2s内的速度增量都是8m/s |
20.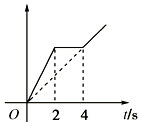 如图所示,表示某一物体的运动图象,由于画图人粗心未标明是v-t图象还是x-t图象,但已知第1s内的速度比第3s内的速度大,下列说法正确的是( )
如图所示,表示某一物体的运动图象,由于画图人粗心未标明是v-t图象还是x-t图象,但已知第1s内的速度比第3s内的速度大,下列说法正确的是( )
 如图所示,表示某一物体的运动图象,由于画图人粗心未标明是v-t图象还是x-t图象,但已知第1s内的速度比第3s内的速度大,下列说法正确的是( )
如图所示,表示某一物体的运动图象,由于画图人粗心未标明是v-t图象还是x-t图象,但已知第1s内的速度比第3s内的速度大,下列说法正确的是( )| A. | 该图一定是v-t图象 | B. | 该图一定是x-t图象 | ||
| C. | 前2s物体的速度越来越大 | D. | 前2s物体的位移越来越大 |

 在如图所示的电路中,电阻R1=3.2Ω,电池组的电动势E=10V,内电阻R=0.8Ω.当电键S断开时,电压表的读数为1.6V,求电阻R2的阻值.
在如图所示的电路中,电阻R1=3.2Ω,电池组的电动势E=10V,内电阻R=0.8Ω.当电键S断开时,电压表的读数为1.6V,求电阻R2的阻值.