题目内容
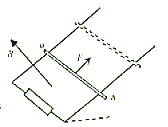
【题目】如图所示,在xOy平面直角坐标系内y轴与垂直x轴的MN边界之间,以x轴为分界线,分别在第Ⅰ、Ⅳ象限有垂直于纸面向外的匀强磁场。第Ⅰ象限内磁场的磁感应强度大小为B0.第Ⅱ象限内有沿x轴正方向的匀强电场,电场强度大小为E. 质量为m、电荷量为q的带正电的粒子从第Ⅱ象限内某点由静止释放,从y轴上的A点进入磁场,经x轴上的B点第一次进入x轴下方的磁场。若已知A点的坐标是(0,a),B点的坐标是(3a,0)，
不考虑粒子重力。
(1)求粒子释放位置与y轴的距离；
(2)若粒子经x轴上方的磁场偏转后不经过y轴仍能回到x轴上方的磁场，求x轴下方磁场的磁感应强度大小应满足的条件；
(3)若x轴下方区域的磁感应强度大小为3B0，且粒子最终垂直于MN边界出射，求MN与x轴交点的坐标。
【答案】（1）
（2）
（3）MN与x轴交点的坐标是（4na，0）（其中n=1，2，3…）
【解析】
（1）设粒子释放位置与y轴的距离为d，粒子在第一象限磁场中做圆周运动的半径为r，画出粒子运动轨迹的示意图，如图所示，
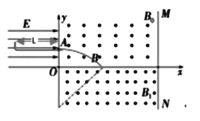
在电场中做匀加速运动，根据动能定理：
①
可得：
粒子在磁场中做圆周运动，根据洛伦兹力提供向心力可得：
②
根据几何关系：(r-a)2+(3a)2=r2③
可得：r=5a
联立①②③式可得：
（2）设粒子进入磁场时与x轴之间的夹角为θ，则粒子在第一象限内的磁场中转过的角度也为θ，
根据几何关系：
，可得：θ=53°
要使粒子经x轴上方的磁场偏转后不经过y轴仍能回到x轴上方的磁场，临界情况如图所示，
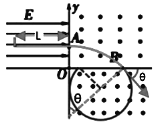
要使粒子经x轴上方的磁场偏转后不经过y轴仍能回到x轴上方的磁场
需满足：3a≥R（1+cos37°） ④
根据洛伦兹力提供向心力可得：
⑤
联立②③④⑤式可得x轴下方磁场的磁感应强度B的大小满足：
（3）设当x轴下方区域的磁感应强度大小为3B0时粒子半径为R′，
根据洛伦兹力提供向心力：
⑥
联立②⑥式可得：
画出粒子运动轨迹的示意图如图所示，
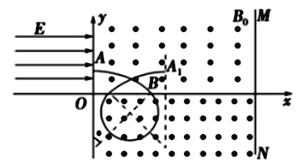
设粒子的速度方向再次与射入磁场时的速度方向一致时的位置为A1，则A与A1的连线与x轴平行，AA1=6a-2 R′sin530
根据几何关系有：AA1=4a
所以粒子最终垂直MN边界飞出，边界MN与y轴间距为
L=nAA1=4 na（其中n=1，2，3…）
即：MN与x轴交点的坐标是（4na，0）（其中n=1，2，3…）
