Question

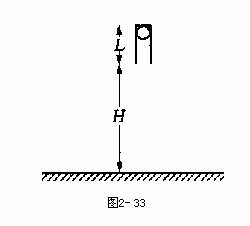
 如图2-33所示，竖直放置的质量为4 m，长为L的圆管顶端塞有一个质量为m的弹性圆球，球和管间的滑动摩擦力和最大静摩擦力大小均为4 mg．圆管从下端离地面距离为H处自由落下，落地后向上弹起的速度与落地时速度大小相等．求：

(1)圆管弹起后圆球不致滑落，L应满足什么条件．

(2)圆管上升的最大高度是多少?

(3)圆管第二次弹起后圆球不致滑落，L又应满足什么条件?

 

 

 

 

Answer 1

 解析：（1）取竖直向下的方向为正方向。

   球与管第一次碰地前瞬间速度，方向向下。

   碰地的瞬间管的速度，方向向上；球的速度，方向向下，

   球相对于管的速度，方向向下。

   碰后，管受重力及向下的摩擦力，加速度a_管=2g，方向向下，

   球受重力及向上的摩擦力，加速度a_球=3g，方向向上，

球相对管的加速度a_相=5g，方向向上。

取管为参照物，则球与管相对静止前，球相对管下滑的距离为：

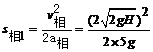
要满足球不滑出圆管，则有。

（2）设管从碰地到它弹到最高点所需时间为t₁（设球与管在这段时间内摩擦力方向不变），则：

设管从碰地到与球相对静止所需时间为t₂，

因为t₁ ＞t₂，说明球与管先达到相对静止，再以共同速度上升至最高点，设球与管达到相对静止时离地高度为h’，两者共同速度为v’，分别为：

然后球与管再以共同速度v’作竖直上抛运动，再上升高度h’’为

因此，管上升最大高度H’=h’+h’’=

（3）当球与管第二次共同下落时，离地高为，球位于距管顶处，同题（1）可解得在第二次反弹中发生的相对位移。