题目内容
 如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B.一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角.设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力.求:
如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B.一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角.设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力.求:(1)电子在磁场中运动轨迹的半径R;(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r.
分析:电子在磁场中受洛伦兹力作用,电子在洛伦兹力作用下做匀速圆周运动,洛伦兹力提供向心力,可以求出电子运动的半径,画出电子运动轨迹,根据几何关系可以求得电子在磁场中的运动的时间和圆形磁场区域的半径.
解答:解:(1)电子在磁场中受到的洛伦兹力提供电子做匀速圆周运动的向心力即:
qvB=m
由此可得电子做圆周运动的半径R=
=
(2)
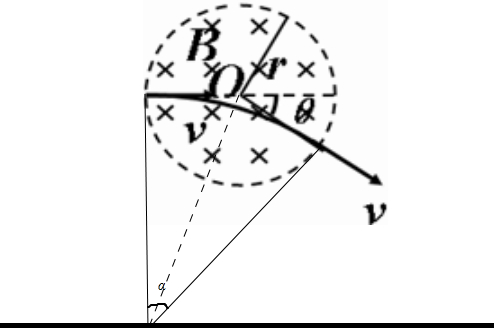
如图根据几何关系,可以知道电子在磁场中做圆周运动对圆心转过的角度α=θ
则电子在磁场中运动的时间:
t=
T=
×
=
×
=
(3)由题意知,由图根据几何关系知:
tan
=
∴r=Rtan
=
tan
答:(1)电子在磁场中运动轨迹的半径R=
;
(2)电子在磁场中运动的时间t=
;
(3)圆形磁场区域的半径r=
tan
.
qvB=m
| v2 |
| R |
由此可得电子做圆周运动的半径R=
| mv |
| qB |
| mv |
| eB |
(2)

如图根据几何关系,可以知道电子在磁场中做圆周运动对圆心转过的角度α=θ
则电子在磁场中运动的时间:
t=
| θ |
| 2π |
| θ |
| 2π |
| 2πR |
| v |
| θ |
| v |
| mv |
| eB |
| mθ |
| eB |
(3)由题意知,由图根据几何关系知:
tan
| θ |
| 2 |
| r |
| R |
∴r=Rtan
| θ |
| 2 |
| mv |
| eB |
| θ |
| 2 |
答:(1)电子在磁场中运动轨迹的半径R=
| mv |
| eB |
(2)电子在磁场中运动的时间t=
| mθ |
| eB |
(3)圆形磁场区域的半径r=
| mv |
| eB |
| θ |
| 2 |
点评:熟悉电子在磁场中做匀速圆周运动由洛伦兹力提供向心力,据此列式求出半径和周期间的表达式,能正确作出电子做圆周运动的半径.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目

