题目内容
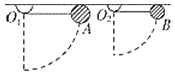
【题目】人造卫星a的圆形轨道离地面高度为h，地球同步卫星b离地面高度为H，h<H，两卫星共面且旋转方向相同．某时刻卫星a恰好出现在赤道上某建筑物c的正上方，设地球赤道半径为R，地面重力加速度为g，则
A. a、b线速度大小之比为
B. a、c角速度之比为
C. b、c向心加速度大小之比
D. a下一次通过c正上方所需时间等于
【答案】C
【解析】试题分析：人造地球卫星绕地球做匀速圆周运动，由地球的万有引力提供向心力，根据牛顿运动定律求解卫星的角速度．卫星绕地球做匀速圆周运动，建筑物随地球自转做匀速圆周运动，当卫星转过的角度与建筑物转过的角度之差等于
时，卫星再次出现在建筑物上空．
绕地球运行的卫星，地球对卫星的万有引力提供向心力，设卫星的线速度为v，则：
，所以
，可知a、b线速度大小之比为
．故A错误；设卫星的角速度为
，
，得
，所以：
，又由于同步卫星b的角速度与c的角速度相同，所以
，故B错误；同步卫星b的角速度与c的角速度相同，根据：
可得：
，故C正确；设经过时间t卫星a再次通过建筑物c上方，根据几何关系有：
，又
，联立解得：
，故D错误．
练习册系列答案
考前必练系列答案
相关题目
