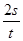题目内容
如图所示是做匀变速直线运动的质点在0~6s内的位移-时间图线.若t=1s时,图线所对应的切线斜率为4(单位:m/s)。则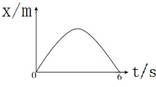
| A.t=1s时,质点在x="2" m的位置 |
| B.t=1s和t=5s时,质点的加速度等大反向 |
| C.t=2s和t=4s时,质点的速率相等 |
| D.前5s内,合外力对质点做正功 |
C
解析试题分析: 由题意可知,t=1s时,速度v1=4m/s,图象对称分布,3s末位移最大,所以3s末速度为零,物体做匀减速直线运动,加速度a=?2m/s2,初速度v0=v1-at=6m/s,所以t=1s时,质点的位移x=v0t+ =5m,故A错误;因为是匀变速直线运动是加速度不变的运动,所以t=1s和t=5s时,质点的加速度是相同的,故B错误;根据对称性可知,t=2s和t=4s时图象的斜率的绝对值相等,则质点的速率相等,故C正确;5s末的速度v5=v0+at5=-4m/s,因为4m/s<6m/s,所以物体动能减小,所以合外力对质点做负功,故D错误.
=5m,故A错误;因为是匀变速直线运动是加速度不变的运动,所以t=1s和t=5s时,质点的加速度是相同的,故B错误;根据对称性可知,t=2s和t=4s时图象的斜率的绝对值相等,则质点的速率相等,故C正确;5s末的速度v5=v0+at5=-4m/s,因为4m/s<6m/s,所以物体动能减小,所以合外力对质点做负功,故D错误.
考点:匀变速直线运动的图像;功的计算.

甲、乙两辆汽车沿平直公路从某地同时同向驶向同一目的地,甲车在前一半时间内以速度v1=3 m/s做匀速运动,后一半时间内以速度v2=6 m/s做匀速运动;乙车在前一半路程中以速度v1=3 m/s做匀速运动,在后一半路程中以速度v2=6 m/s做匀速运动,则可知( )
| A.甲的平均速度大于乙的平均速度 |
| B.甲行驶全程所用时间大于乙行驶全程所用时间 |
| C.甲的平均速度小于乙的平均速度 |
| D.甲行驶全程所用时间小于乙行驶全程所用时间 |
在平直轨道上匀加速向右行驶的封闭车厢中,悬挂着一个带有滴管的盛油容器,如图所示.当滴管依次滴下三滴油时(设三滴油都落在车厢底板上),下列说法中正确的是
| A.这三滴油依次落在OA之间,且后一滴比前一滴离O点远 |
| B.这三滴油依次落在OA之间,且后一滴比前一滴离O点近 |
| C.这三滴油依次落在O点上 |
| D.这三滴油依次落在OA间同一位置上 |
一质点沿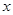 轴运动,其位置
轴运动,其位置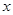 随时间
随时间 变化的规律为:
变化的规律为: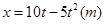 ,
, 的单位为s。下列关于该质点运动的说法正确的是( )
的单位为s。下列关于该质点运动的说法正确的是( )
| A.该质点的加速度大小为5m/s2 | B.物体回到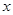 =0处时其速度大小为10m/s =0处时其速度大小为10m/s |
| C.t= 2s时刻该质点速度为零 | D.0~3s内该质点的平均速度大小为5m/s |
物体静止在光滑水平面上,先对物体施加一水平向右的恒力F1,经时间t后撤去F1,立即再对它施加一水平向左的恒力F2,又经时间3t后物体回到出发点,在这一过程中,F1、F2分别对物体做的功W1、W2间的关系是( )
| A.W1∶W2=1∶1 | B.W1∶W2=2∶3 | C.W1∶:W2=9∶5 | D.W1∶W2=9∶7 |
伽利略曾说过:“科学是在不断改变思维角度的探索中前进的”。他在著名的斜面实验中,让小球分别沿倾角不同、阻力很小的斜面从静止开始滚下,他通过实验观察和逻辑推理,得到的正确结论有
| A.倾角一定时,小球在斜面上的速度与时间的平方成正比 |
| B.倾角一定时,小球在斜面上的位移与时间的平方成正比 |
| C.斜面长度一定时,小球从顶端滚到底端时的速度与倾角无关 |
| D.斜面长度一定时,小球从顶端滚到底端所需的时间与倾角无关 |
如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ,则下列说法正确的是
A. = =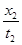 = = | B. > >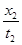 > > |
C. = = = = | D.若θ增大,则 的值减小 的值减小 |
足够长的光滑绝缘槽,与水平方向的夹角分别为α和β(α<β),如图所示,加垂直于纸面向里的磁场,分别将质量相等,带等量正、负电荷的小球a和b,依次从两斜面的顶端由静止释放,关于两球在槽上的运动,下列说法中不正确的是( ) 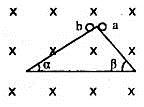
| A.在槽上a.b两球都做匀加速直线运动,aa>ab |
| B.在槽上a、b两球都做变加速直线运动,但总有aa>ab |
| C.a、b两球沿槽运动的时间分别为ta、、tb则ta<tb |
| D.a,b两球沿斜面运动的最大竖直高度分别为ha、hb,则ha<hb |