题目内容
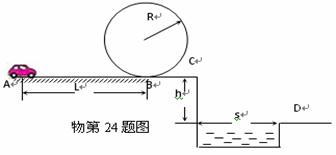
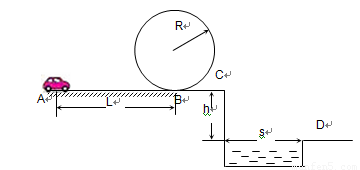
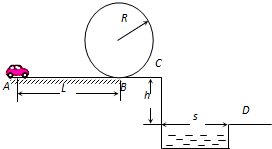 一电动小车沿如图所示的路径运动,小车从A点以5.0W的恒定功率由静止启动,沿粗糙的水平直轨道运动L后,由B点进入半径为R的光滑竖直圆形轨道,运动一周后又从B点离开圆轨道进入水平光滑轨道BC段,在C与平面D间是一蓄水池.已知小车质量m=1.0kg、L=10m、R=0.32m、h=1.25m、s=1.50m,在AB段所受阻力为0.7N.小车只在AB路段可以施加牵引力,其他路段电动机关闭.问:要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台上,小车电动机至少工作多长时间?(g取10m/s2)
一电动小车沿如图所示的路径运动,小车从A点以5.0W的恒定功率由静止启动,沿粗糙的水平直轨道运动L后,由B点进入半径为R的光滑竖直圆形轨道,运动一周后又从B点离开圆轨道进入水平光滑轨道BC段,在C与平面D间是一蓄水池.已知小车质量m=1.0kg、L=10m、R=0.32m、h=1.25m、s=1.50m,在AB段所受阻力为0.7N.小车只在AB路段可以施加牵引力,其他路段电动机关闭.问:要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台上,小车电动机至少工作多长时间?(g取10m/s2)分析:车刚好越过圆轨道最高点,由牛顿第二定律求得在最高点的临界速度.由机械能守恒定律研究从B点到最高点求得B点速度.
小车离开C点后做平抛运动,要落在右侧平台上,水平位移至少为s,即可分析B点的速度应满足什么条件,再对AB段由动能定理求得小车电动机工作时间.
小车离开C点后做平抛运动,要落在右侧平台上,水平位移至少为s,即可分析B点的速度应满足什么条件,再对AB段由动能定理求得小车电动机工作时间.
解答:解:设车刚好越过圆轨道最高点,设最高点速度为v2,最低点速度为v1
在最高点由牛顿第二定律得:mg=
从B点运动到最高点由机械能守恒定律得:
mv12=
mv22+mg×(2R)
小车离开C点后做平抛运动由h=
gt2
得:t=
=
s=0.5s
则x=v1t=2m
因为x>s,所以小车能够越过蓄水池.
设电动机工作时间为t0,在AB段由动能定理得:
Pt0-fL=
mv12
解得:t0=3.0s
答:要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台上,小车电动机至少工作3.0s.
在最高点由牛顿第二定律得:mg=
| mv22 |
| R |
从B点运动到最高点由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
小车离开C点后做平抛运动由h=
| 1 |
| 2 |
得:t=
|
|
则x=v1t=2m
因为x>s,所以小车能够越过蓄水池.
设电动机工作时间为t0,在AB段由动能定理得:
Pt0-fL=
| 1 |
| 2 |
解得:t0=3.0s
答:要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台上,小车电动机至少工作3.0s.
点评:本题很好的把平抛运动和圆周运动结合在一起运用动能定理解决,能够很好的考查学生的能力,关键要把握住圆周运动最高点的临界条件.

练习册系列答案
相关题目
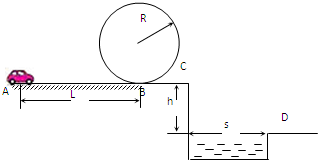 一电动小车沿如图所示的路径运动,小车从A点由静止出发,沿粗糙的水平直轨道运动L后,由B点进入半径为R的光滑竖直圆形轨道,运动一周后又从B点离开圆轨道进入水平光滑轨道BC段,在C与平面D间是一蓄水池.已知小车质量m=0.1kg、L=10m、R=0.32m、h=1.25m、s=1.50m,在AB段所受阻力为0.3N.小车只在AB路段可以施加牵引力,牵引力的功率为P=1.5W,其他路段电动机关闭.问:要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台D上,小车电动机至少工作多长时间?(g取10m/s2)
一电动小车沿如图所示的路径运动,小车从A点由静止出发,沿粗糙的水平直轨道运动L后,由B点进入半径为R的光滑竖直圆形轨道,运动一周后又从B点离开圆轨道进入水平光滑轨道BC段,在C与平面D间是一蓄水池.已知小车质量m=0.1kg、L=10m、R=0.32m、h=1.25m、s=1.50m,在AB段所受阻力为0.3N.小车只在AB路段可以施加牵引力,牵引力的功率为P=1.5W,其他路段电动机关闭.问:要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台D上,小车电动机至少工作多长时间?(g取10m/s2)