题目内容
15. 2013年10月25日我国成功将:“实践十六号”卫星送入预定轨道.如图所示,“实践十六号”卫星的发射过程可简化为:卫星发射后,先在椭圆轨道上运行一段时间,再稳定在对应的圆轨道上,稳定后,若“实践十六号”卫星的运动可看做在距离地面高度为h的轨道上做匀速圆周运动.已知地球半径为R,地球表面的重力加速度为g.卫星在椭圆轨道上运行时,地心处在椭圆的一个焦点上.则下列说法正确的是( )
2013年10月25日我国成功将:“实践十六号”卫星送入预定轨道.如图所示,“实践十六号”卫星的发射过程可简化为:卫星发射后,先在椭圆轨道上运行一段时间,再稳定在对应的圆轨道上,稳定后,若“实践十六号”卫星的运动可看做在距离地面高度为h的轨道上做匀速圆周运动.已知地球半径为R,地球表面的重力加速度为g.卫星在椭圆轨道上运行时,地心处在椭圆的一个焦点上.则下列说法正确的是( )| A. | “实践十六号”在圆轨道上运行的加速度大小是$\frac{g{R}^{2}}{{h}^{2}}$ | |
| B. | “实践十六号”在圆轨道上从A到B的运行时间是π$\sqrt{\frac{(2R+h)^{3}}{8g{R}^{2}}}$ | |
| C. | “实践十六号”在圆轨道上运行的速度大小是R$\sqrt{\frac{g}{R}}$ | |
| D. | “实践十六号”在B点从椭圆轨道进入圆轨道时需减速 |
分析 根据万有引力提供向心力和根据万有引力等于重力列出等式进行比较求解.
解答 解:A、根据万有引力提供向心力有:$G\frac{Mm}{{r}^{2}}=ma$,r=R+h,
根据万有引力等于重力得:$G\frac{Mm}{{R}^{2}}=mg$
所以“实践十六号”在圆轨道上运行的加速度是$\frac{g{R}^{2}}{(R+h)^{2}}$,故A错误;
B、根据开普勒周期定律可得$\frac{(\frac{2R+h}{2})^{3}}{{T}^{2}}=\frac{{R}^{3}}{T{′}^{2}}$,其中T′为近地卫星的周期$T′=2π\sqrt{\frac{{R}^{3}}{GM}}=2π\sqrt{\frac{{R}^{3}}{{R}^{2}g}}=2π\sqrt{\frac{R}{g}}$,所以$T=2π\sqrt{\frac{(2R+h)^{3}}{8g{R}^{2}}}$,故“实践十六号”在椭圆轨道上从A到B的运行时间是$\frac{T}{2}$=π$\sqrt{\frac{(2R+h)^{3}}{8g{R}^{2}}}$,故B正确;
C、根据万有引力提供向心力有:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,得$v=\sqrt{\frac{GM}{r}}$=R$\sqrt{\frac{g}{R+h}}$,故C错误;
D、“实践十六号”进入圆轨道前需加速,做离心运动,故D错误;
故选:B.
点评 解决本题的关键知道卫星运动的特点,以及掌握万有引力提供向心力这一理论,并能熟练运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
3. 某同学在探究加速度a与物体质量M的关系时,测出了表中数据,
某同学在探究加速度a与物体质量M的关系时,测出了表中数据,
(1)请在图中坐标上作出a-$\frac{1}{M}$图象
(2)为了研究加速度跟力和质量的关系,应该采用的研究实验方法是A
A.控制变量法 B.假设法 C.理想实验法 D.图象法
(3)如果加速度跟质量的倒数的关系图象是通过原点的一条直线,则说明物体的加速度与与物体的质量成反比.
 某同学在探究加速度a与物体质量M的关系时,测出了表中数据,
某同学在探究加速度a与物体质量M的关系时,测出了表中数据,| 1/M | 2.00 | 2.50 | 3.33 | 4.00 | 4.80 |
| a/m•s-2 | 0.44 | 0.56 | 0.73 | 0.89 | 1.08 |
(2)为了研究加速度跟力和质量的关系,应该采用的研究实验方法是A
A.控制变量法 B.假设法 C.理想实验法 D.图象法
(3)如果加速度跟质量的倒数的关系图象是通过原点的一条直线,则说明物体的加速度与与物体的质量成反比.
3. 如图所示,一小物块由粗糙斜面上的O点静止释放,下滑过程中经过A、B两点;若小物块改由O′点静止释放,再次经过A、B两点,小物块第二次从A到B的过程中与第一次相比( )
如图所示,一小物块由粗糙斜面上的O点静止释放,下滑过程中经过A、B两点;若小物块改由O′点静止释放,再次经过A、B两点,小物块第二次从A到B的过程中与第一次相比( )
 如图所示,一小物块由粗糙斜面上的O点静止释放,下滑过程中经过A、B两点;若小物块改由O′点静止释放,再次经过A、B两点,小物块第二次从A到B的过程中与第一次相比( )
如图所示,一小物块由粗糙斜面上的O点静止释放,下滑过程中经过A、B两点;若小物块改由O′点静止释放,再次经过A、B两点,小物块第二次从A到B的过程中与第一次相比( )| A. | 摩擦力对小物块的冲量变大 | B. | 摩擦力对小物块的冲量变小 | ||
| C. | 小物块的动能改变量变大 | D. | 小物块的动能改变量变小 |
7. 如图所示,在投球游戏中,某人将小球从P点以速度v水平抛向固定在水平地面上的塑料筐,小球恰好沿着筐的上沿入筐并打在筐的底角,若要让小球进入筐中并直接击中筐底正中间,下列说法可行的是( )
如图所示,在投球游戏中,某人将小球从P点以速度v水平抛向固定在水平地面上的塑料筐,小球恰好沿着筐的上沿入筐并打在筐的底角,若要让小球进入筐中并直接击中筐底正中间,下列说法可行的是( )
 如图所示,在投球游戏中,某人将小球从P点以速度v水平抛向固定在水平地面上的塑料筐,小球恰好沿着筐的上沿入筐并打在筐的底角,若要让小球进入筐中并直接击中筐底正中间,下列说法可行的是( )
如图所示,在投球游戏中,某人将小球从P点以速度v水平抛向固定在水平地面上的塑料筐,小球恰好沿着筐的上沿入筐并打在筐的底角,若要让小球进入筐中并直接击中筐底正中间,下列说法可行的是( )| A. | 在P点将小球以小于v的速度水平抛出 | |
| B. | 在P点将小球以大于v的速度水平抛出 | |
| C. | 在P点正上方某位置将小球以小于v的速度水平抛出 | |
| D. | 在P点正下方某位置将小球以小于v的速度水平抛出 |
4. 某质点在恒力F作用下,从A点沿图中曲线方向运动的B点,到达B点后,质点受到的力大小仍为F,但方向相反,则它从B点开始的运动轨迹可能是图中的哪条曲线( )
某质点在恒力F作用下,从A点沿图中曲线方向运动的B点,到达B点后,质点受到的力大小仍为F,但方向相反,则它从B点开始的运动轨迹可能是图中的哪条曲线( )
 某质点在恒力F作用下,从A点沿图中曲线方向运动的B点,到达B点后,质点受到的力大小仍为F,但方向相反,则它从B点开始的运动轨迹可能是图中的哪条曲线( )
某质点在恒力F作用下,从A点沿图中曲线方向运动的B点,到达B点后,质点受到的力大小仍为F,但方向相反,则它从B点开始的运动轨迹可能是图中的哪条曲线( )| A. | 曲线a | B. | 直线b | ||
| C. | 曲线c | D. | 三条曲线都有可能 |

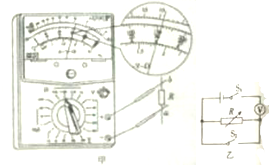 多用电表是实验室和生产实际中常用的仪器之一,它具有测量电压、电流及电阻等多种测量功能.
多用电表是实验室和生产实际中常用的仪器之一,它具有测量电压、电流及电阻等多种测量功能. 为多用电表(选择开关置于直流“2.5V”挡)
为多用电表(选择开关置于直流“2.5V”挡) 如图,光滑水平面上有一质量为M的平板车,其上表面是一段长为L的粗糙水平轨道,左侧连一半径为R的$\frac{1}{4}$光滑圆弧轨道.圆弧轨道与水平轨道在O′点相切.车右端竖直墙壁固定一个处于锁定状态的弹簧,质量为m的小物块(可视为质点)处于车的右端紧靠弹簧放置,小物块与水平轨道间的动摩擦因数μ,整个装置处于静止状态,现将弹簧解除锁定,小物块在极短时间内被弹出,恰能到达圆弧轨道的最高点A.之后又从A点滑下,已知M=4m,重力加速度为g,若小物块最终不会滑离小车,求小物块与车相对静止时的速度及其与车右端点的距离x.
如图,光滑水平面上有一质量为M的平板车,其上表面是一段长为L的粗糙水平轨道,左侧连一半径为R的$\frac{1}{4}$光滑圆弧轨道.圆弧轨道与水平轨道在O′点相切.车右端竖直墙壁固定一个处于锁定状态的弹簧,质量为m的小物块(可视为质点)处于车的右端紧靠弹簧放置,小物块与水平轨道间的动摩擦因数μ,整个装置处于静止状态,现将弹簧解除锁定,小物块在极短时间内被弹出,恰能到达圆弧轨道的最高点A.之后又从A点滑下,已知M=4m,重力加速度为g,若小物块最终不会滑离小车,求小物块与车相对静止时的速度及其与车右端点的距离x.