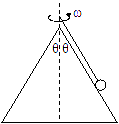题目内容
如图光滑的圆锥顶端，用长为L=2m的细绳悬一质量为m=1kg的小球，圆锥顶角为2θ=74°，求：
（1）当小球以ω=1rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力；
（2）当小球以ω=5rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力。
（1）当小球以ω=1rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力；
（2）当小球以ω=5rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力。
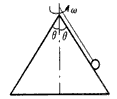
解：小球在圆锥面上运动时，受到重力G、细绳的拉力T和斜面的支持力N。将这些力分解在水平方向和竖直方向上，有Tsinθ－Ncosθ＝mω2Lsinθ，Tcosθ＋Nsinθ＝mg。设小球以角速度ω0转动时，小球刚好离开斜面，此时，由N=0代入上述两式得ω0=
rad/s
（1）当小球以ω=1rad/s转动时，小球在斜面上运动，由上述两式得T=（mω2Ltanθsinθ－mg）/（tanθsinθ－cosθ）=26N
（2）当小球以ω=5rad/s转动时，小球将离开斜面，此时受到拉力和重力，设细绳与竖直方向得夹角为α，则Tsinα=mω2Lsinα，代入数据解得T=50N
rad/s（1）当小球以ω=1rad/s转动时，小球在斜面上运动，由上述两式得T=（mω2Ltanθsinθ－mg）/（tanθsinθ－cosθ）=26N
（2）当小球以ω=5rad/s转动时，小球将离开斜面，此时受到拉力和重力，设细绳与竖直方向得夹角为α，则Tsinα=mω2Lsinα，代入数据解得T=50N
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
如图乙所示，将其中一质量为m的小球仍与一长为L的细绳连接，放在表面光滑的正圆锥体表面，上端可绕圆锥顶点自由转动。圆锥体放在水平面上，其轴线沿竖直方向，圆锥母线与轴线之间夹角α为30°，试求：
绕圆锥轴线做水平匀速圆周运动而圆柱M不动时，圆柱与两接触面间的摩擦因数μ至少多大？