题目内容
 (2011?河西区二模)如图所示(俯视图),相距为2L的光滑平行金属导轨水平放置,导轨一部分处在以OO′为右边界的匀强磁场中,匀强磁场的磁感应强大小为B,方向垂直导轨平面向下,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距边界OO′为L处垂直导轨放置一质量为m、电阻不计的金属杆ab.求解以下问题:
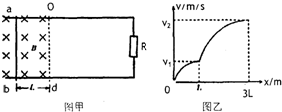
(2011?河西区二模)如图所示(俯视图),相距为2L的光滑平行金属导轨水平放置,导轨一部分处在以OO′为右边界的匀强磁场中,匀强磁场的磁感应强大小为B,方向垂直导轨平面向下,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距边界OO′为L处垂直导轨放置一质量为m、电阻不计的金属杆ab.求解以下问题:(1)若金属杆ab固定在导轨上的初始位置.磁场的磁感应强度在时间t内由B均匀减小到零.求此过程中电阻R上产生的焦耳热Ql.
(2)若磁场的磁感应强度不变,金属杆ab在恒力作用下由静止开始向右运动3L距离,其V--X的关系图象如图乙所示.求:
①金属杆ab刚要离开磁场时的加速度大小;
②此过程中电阻R上产生的焦耳热Q2.
分析:根据法拉第电磁感应定律求出线框中感应电动势.
根据焦耳定律求出电阻R上产生的焦耳热Ql.
对金属杆ab进行受力分析和运动过程分析,应用动能定理研究从L到3L的过程,表示出恒力F.
对金属杆ab刚要离开磁场时进行受力分析,运用牛顿第二定律列出等式求出加速度.
运用动能定理研究由起始位置到发生位移L的过程,求出安培力做功.
根据功能关系知道克服安培力做功求出电路中产生的焦耳热.
根据焦耳定律求出电阻R上产生的焦耳热Ql.
对金属杆ab进行受力分析和运动过程分析,应用动能定理研究从L到3L的过程,表示出恒力F.
对金属杆ab刚要离开磁场时进行受力分析,运用牛顿第二定律列出等式求出加速度.
运用动能定理研究由起始位置到发生位移L的过程,求出安培力做功.
根据功能关系知道克服安培力做功求出电路中产生的焦耳热.
解答:解:(1)磁场的磁感应强度在时间t内由B均匀减小到零,说明
=
根据法拉第电磁感应定律得出此过程中的感应电动势为:
E1=
=
①
通过R的电流为I1=
②
此过程中电阻R上产生的焦耳热为Q1=I12Rt ③
联立求得Q1=
(2)①ab杆离起始位置的位移从L到3L的过程中,由动能定理可得:
F(3L-L)=
m(v22-v12) ④
ab杆刚要离开磁场时,感应电动势 E2=2BLv1 ⑤
通过R的电流为I2=
⑥
ab杆水平方向上受安培力F安和恒力F作用,安培力为:
F安=2BI2L ⑦
联立⑤⑥⑦F安=
⑧
由牛顿第二定律可得:F-F安=ma ⑨
联立④⑧⑨解得a=
-
②ab杆在磁场中由起始位置到发生位移L的过程中,由动能定理可得:
FL+W安=
mv12-0
W安=
mv12-FL ⑩
根据功能关系知道克服安培力做功等于电路中产生的焦耳热,
所以联立④⑩解得 Q2=-W安=
答:(1)若金属杆ab固定在导轨上的初始位置.磁场的磁感应强度在时间t内由B均匀减小到零.此过程中电阻R上产生的焦耳热为
.
(2)①金属杆ab刚要离开磁场时的加速度大小是
-
;
②此过程中电阻R上产生的焦耳热为
.
| △B |
| △t |
| B |
| t |
根据法拉第电磁感应定律得出此过程中的感应电动势为:
E1=
| △Φ |
| △t |
| 2BL2 |
| t |
通过R的电流为I1=
| E1 |
| R |
此过程中电阻R上产生的焦耳热为Q1=I12Rt ③
联立求得Q1=
| 4B2L4 |
| Rt |
(2)①ab杆离起始位置的位移从L到3L的过程中,由动能定理可得:
F(3L-L)=
| 1 |
| 2 |
ab杆刚要离开磁场时,感应电动势 E2=2BLv1 ⑤
通过R的电流为I2=
| E2 |
| R |
ab杆水平方向上受安培力F安和恒力F作用,安培力为:
F安=2BI2L ⑦
联立⑤⑥⑦F安=
| 4B2L2v1 |
| R |
由牛顿第二定律可得:F-F安=ma ⑨
联立④⑧⑨解得a=
| v22-v12 |
| 4L |
| 4B2L2v1 |
| mR |
②ab杆在磁场中由起始位置到发生位移L的过程中,由动能定理可得:
FL+W安=
| 1 |
| 2 |
W安=
| 1 |
| 2 |
根据功能关系知道克服安培力做功等于电路中产生的焦耳热,
所以联立④⑩解得 Q2=-W安=
| m(v22-3v12) |
| 4 |
答:(1)若金属杆ab固定在导轨上的初始位置.磁场的磁感应强度在时间t内由B均匀减小到零.此过程中电阻R上产生的焦耳热为
| 4B2L4 |
| Rt |
(2)①金属杆ab刚要离开磁场时的加速度大小是
| v22-v12 |
| 4L |
| 4B2L2v1 |
| mR |
②此过程中电阻R上产生的焦耳热为
| m(v22-3v12) |
| 4 |
点评:要能够把法拉第电磁感应定律与电路知识结合运用.
电磁感应中动力学问题离不开受力分析和运动过程分析.
关于电磁感应中能量问题我们要从功能关系角度出发研究.
电磁感应中动力学问题离不开受力分析和运动过程分析.
关于电磁感应中能量问题我们要从功能关系角度出发研究.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
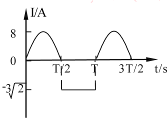 (2011?河西区二模)某电阻元件在正常工作时,通过它的电流按如图所示的规律变化.今与这个电阻元件串联一个电流表,则电流表的数为( )
(2011?河西区二模)某电阻元件在正常工作时,通过它的电流按如图所示的规律变化.今与这个电阻元件串联一个电流表,则电流表的数为( ) (2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( )
(2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( ) 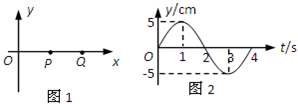 (2011?河西区二模)如图1所示,一根水平张紧弹性长绳上有等间距的O、P、Q质点,相邻两质点间距离为1.0m.t=0时刻O质点从平衡位置开始沿y轴方向振动,并产生沿x轴正方向传播的波,O质点的振动图象如图2所示.当O质点第一次达到正向最大位移时,P质点刚开始振动,则( )
(2011?河西区二模)如图1所示,一根水平张紧弹性长绳上有等间距的O、P、Q质点,相邻两质点间距离为1.0m.t=0时刻O质点从平衡位置开始沿y轴方向振动,并产生沿x轴正方向传播的波,O质点的振动图象如图2所示.当O质点第一次达到正向最大位移时,P质点刚开始振动,则( )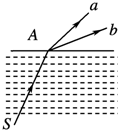 (2011?河西区二模)蓝光光碟是利用波长较短(波长约为405nm)的蓝色激光读取和写入数据的光碟,而传统DVD需要光头发出红色激光(波长约为650nm)来读取或写入数据,通常来说波长越短的激光,能够在单位面积上记录或读取更多的信息.因此,蓝光极大地提高了光盘的存储容量,对于光存储产品来说,蓝光提供了一个跳跃式发展的机会.目前为止,蓝光是最先进的大容量光碟格式.一束由红、蓝两单色激光组成的复色光从水中射向空气中,并分成a、b两束,则下列说法正确的是( )
(2011?河西区二模)蓝光光碟是利用波长较短(波长约为405nm)的蓝色激光读取和写入数据的光碟,而传统DVD需要光头发出红色激光(波长约为650nm)来读取或写入数据,通常来说波长越短的激光,能够在单位面积上记录或读取更多的信息.因此,蓝光极大地提高了光盘的存储容量,对于光存储产品来说,蓝光提供了一个跳跃式发展的机会.目前为止,蓝光是最先进的大容量光碟格式.一束由红、蓝两单色激光组成的复色光从水中射向空气中,并分成a、b两束,则下列说法正确的是( )