题目内容
 (2011?甘肃模拟)如图所示,从地面上A点发射一枚远程弹道导弹,在引力作用下,沿ACB椭圆轨道飞行击中地面目标B,C为轨道的远地点,距地面高度为h.已知地球半径为R,地球质量为m地,引力常量为G.设距地面高度为h的圆轨道上卫星运动周期为T0,不计空气阻力.下列结论正确的是( )
(2011?甘肃模拟)如图所示,从地面上A点发射一枚远程弹道导弹,在引力作用下,沿ACB椭圆轨道飞行击中地面目标B,C为轨道的远地点,距地面高度为h.已知地球半径为R,地球质量为m地,引力常量为G.设距地面高度为h的圆轨道上卫星运动周期为T0,不计空气阻力.下列结论正确的是( )分析:A、若在C点能够做匀速圆周运动,提供的万有引力等于需要的向心力,现在做近心运动,可见提供的万有引力大于需要的向心力,C点的速度小于在C点做匀速圆周运动的速度.
B、先求出在C点受到的万有引力,再根据牛顿第二定律求加速度.
C、导弹做的是椭圆运动,地球位于椭圆的焦点上.
D、根据开普勒第三定律比较椭圆轨道和圆轨道的周期.
B、先求出在C点受到的万有引力,再根据牛顿第二定律求加速度.
C、导弹做的是椭圆运动,地球位于椭圆的焦点上.
D、根据开普勒第三定律比较椭圆轨道和圆轨道的周期.
解答:解:A、根据G
=m
,在C点做匀速圆周运动的速度v=
.因为做椭圆运动,在C点提供的力大于所需要的向心力,所以导弹在C点的速度小于
.故A错.
B、导弹在C点受到的万有引力F=G
,所以a=
=G
.故B正确.
C、导弹做的是椭圆运动,地球位于椭圆的焦点上.故C正确.
D、根据开普勒第三定律,
=C,椭圆轨道的半长轴小于圆轨道的半径,所以椭圆的周期小于圆的周期,所以导弹从点A运动到B点的时间一定小于T0.故D正确.
故选BCD.
| m地m |
| (R+h)2 |
| v2 |
| R+h |
|
|
B、导弹在C点受到的万有引力F=G
| m地m |
| (R+h)2 |
| F |
| m |
| m地 |
| (R+h)2 |
C、导弹做的是椭圆运动,地球位于椭圆的焦点上.故C正确.
D、根据开普勒第三定律,
| R3 |
| T2 |
故选BCD.
点评:解决本题的关键掌握万有引力提供向心力G
=m
,以及开普勒第三定律
=C.
| m地m |
| (R+h)2 |
| v2 |
| R+h |
| R3 |
| T2 |

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目

 (2011?甘肃模拟)如图所示,光滑水平面上有A、B、C三个物块,其质量分别为mA=2.0kg,mB=1.0kg,mC=1.0kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功108J(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求
(2011?甘肃模拟)如图所示,光滑水平面上有A、B、C三个物块,其质量分别为mA=2.0kg,mB=1.0kg,mC=1.0kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功108J(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求 (2011?甘肃模拟)如图16所示,一轻质弹簧竖直固定在地面上,自然长度为1m,上面连接一个质量为m1=1kg的物体,平衡时物体离地面0.9m.距物体m1正上方高为0.3m处有一个质量为m2=1kg的物体自由下落后与弹簧上物体m1碰撞立即合为一体,一起在竖直面内做简谐振动.当弹簧压缩量最大时,弹簧长为0.6m.求(g取10m/s2):
(2011?甘肃模拟)如图16所示,一轻质弹簧竖直固定在地面上,自然长度为1m,上面连接一个质量为m1=1kg的物体,平衡时物体离地面0.9m.距物体m1正上方高为0.3m处有一个质量为m2=1kg的物体自由下落后与弹簧上物体m1碰撞立即合为一体,一起在竖直面内做简谐振动.当弹簧压缩量最大时,弹簧长为0.6m.求(g取10m/s2):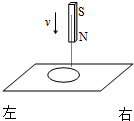 (2011?甘肃模拟)如图所示,光滑绝缘水平面上有一个静止的小导体环,现在将一个条形磁铁从导体环的右上方较高处突然向下移动,则在此过程中,关于导体环的运动方向以及导体环中的电流方向,下列说法中正确的是( )
(2011?甘肃模拟)如图所示,光滑绝缘水平面上有一个静止的小导体环,现在将一个条形磁铁从导体环的右上方较高处突然向下移动,则在此过程中,关于导体环的运动方向以及导体环中的电流方向,下列说法中正确的是( )