题目内容
16. 如图所示,质量M=10kg的木块ABC静置于粗糙的水平底面上,在木块的倾角θ=30°的斜面上,有一质量m=1.0kg的物块由静止开始沿斜面下滑,当滑行位移s=1.4m时,其速度v=1.4m/s,在此过程中木块保持静止不动.求地面对木块的摩擦力和支持力的大小与方向.(取g=10m/s2)
如图所示,质量M=10kg的木块ABC静置于粗糙的水平底面上,在木块的倾角θ=30°的斜面上,有一质量m=1.0kg的物块由静止开始沿斜面下滑,当滑行位移s=1.4m时,其速度v=1.4m/s,在此过程中木块保持静止不动.求地面对木块的摩擦力和支持力的大小与方向.(取g=10m/s2)
分析 物块沿斜面向下做匀加速运动,垂直于斜面方向力平衡,由此求斜面对木块的支持力.沿斜面方向,根据运动学公式求出加速度.根据牛顿第二定律列式求出物块所受的摩擦力,再对木块M进行受力分析,根据平衡条件求解地面对木块的摩擦力和支持力.
解答  解:对物块m:初速度v0=0,位移x=1.4m.末速度v=1.4m/s,
解:对物块m:初速度v0=0,位移x=1.4m.末速度v=1.4m/s,
由v2-v02=2as
得:a=$\frac{{v}^{2}}{2a}$=$\frac{1.{4}^{2}}{2×1.4}$=0.7m/s2
由于垂直于斜面方向没有加速度,受力平衡,则有:
垂直斜面方向有:FN=mgcos30°=1×10×$\frac{\sqrt{3}}{2}$N=5$\sqrt{3}$N
沿斜面方向有:mgsin30°-f=ma
解得:f=mgsin30°-ma=1×10×0.5-0.7=4.3N
对木块,根据牛顿第三定律得:
物块m对木块M的压力为 FN′=FN=5$\sqrt{3}$N,摩擦力 f′=f=4.3N
设地面对木块M的摩擦力水平向左.则:
根据平衡条件,在竖直方向,有:FN地=Mg+FN′cosθ+f′sinθ=100+5$\sqrt{3}$×$\frac{\sqrt{3}}{2}$+4.3×0.5=109.65N.方向竖直向上.
水平方向有:f′=FN′sinθ-f′cosθ=mgcos30°sin30°-(mgsin30°-macos30°)=macos30°=1×0.7×$\frac{\sqrt{3}}{2}$N=$\frac{7}{20}\sqrt{3}$N,方向水平向左.
答:地面对木块的摩擦力大小为$\frac{7}{20}\sqrt{3}$N,方向水平向左,支持力的大小是109.65N.方向竖直向上.
点评 本题主要考查了牛顿第二定律及运动学基本公式的直接应用,要求同学们能正确对物块进行受力分析,运用隔离法研究.

| A. | 卡文迪许测出了静电力常量k的数值 | |
| B. | 第谷总结出了行星运动的三大定律 | |
| C. | 牛顿总结出了万有引力定律 | |
| D. | 法拉第总结出了库仑定律 |
 矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中,输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中,输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )| A. | 1s末线框平面垂直于磁场,穿过线框的磁通量变化最快 | |
| B. | 2s末线框平面垂直于磁场,穿过线框的磁通量最大 | |
| C. | 交流电压的有效值为36$\sqrt{2}$V,频率为0.25Hz | |
| D. | 用该交流电为额定电压36V的机床照明灯供电,照明灯恰好可以正常发光 |
| A. | 匀速直线运动 | B. | 匀变速直线运动 | C. | 匀速圆周运动 | D. | 匀变速曲线运动 |

| A. | 线圈A向上移动或滑动变阻器滑动触头P向右加速滑动都能引起电流计指针左偏 | |
| B. | 线圈A中铁芯向上拔出或断开开关,都能引起电流计指针右偏 | |
| C. | 滑动变阻器的滑动触头P匀速向左或匀速向右滑动,都能使电流计指针静止在中央 | |
| D. | 因为线圈A、线圈B的绕线方向未知,故无法判断电流计指针偏转的方向 |
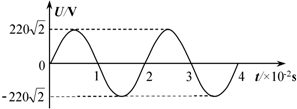
| A. | 交变电流的频率为2Hz | B. | 交变电流的周期为2s | ||
| C. | 交变电压的最大值为220$\sqrt{2}$V | D. | 交变电压的有效值为220$\sqrt{2}$V |
(1)他们应选用图1的哪个电路进行实验?A

(2)实验测得元件Z的电压与电流的关系如表所示.
| U/V | 0 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.50 | 1.60 |
| I/A | 0 | 0.20 | 0.45 | 0.80 | 1.25 | 1.80 | 2.80 | 3.20 |
(3)用螺旋测微器测得线状元件Z的直径如图2所示,则元件Z的直径是1.990mm;
(4)把元件Z接入如图3所示的电路中,当电阻R的阻值为2Ω时电流表的读数为1.25A;当电阻R的阻值为3.6Ω时电流表的读数为0.80A.结合上表数据可求得电池的电动势为E=4V,内阻为r=0.4Ω.
 如图所示,倾角为θ的直角斜面体固定在水平地面上,其顶端固定有一轻质定滑轮,轻质弹簧和轻质细绳相连,一端接质量为m2的物块B,物块B放在地面上且使滑轮和物块间的细绳竖直,一端连接质量为m1的物块A,物块A放在光滑斜面上的P点保持静止,弹簧和斜面平行,此时弹簧具有的弹性势能为Ep.不计定滑轮、细绳、弹簧的质量,不计斜面、滑轮的摩擦,已知弹簧劲度系数为k,P点到斜面底端的距离为L.现将物块A缓慢斜向上移动,直到弹簧刚恢复原长时的位置,并由静止释放物块A,当物块B刚要离开地面时,物块A的速度即变为零,求:在以后的运动过程中物块A最大速度的大小.
如图所示,倾角为θ的直角斜面体固定在水平地面上,其顶端固定有一轻质定滑轮,轻质弹簧和轻质细绳相连,一端接质量为m2的物块B,物块B放在地面上且使滑轮和物块间的细绳竖直,一端连接质量为m1的物块A,物块A放在光滑斜面上的P点保持静止,弹簧和斜面平行,此时弹簧具有的弹性势能为Ep.不计定滑轮、细绳、弹簧的质量,不计斜面、滑轮的摩擦,已知弹簧劲度系数为k,P点到斜面底端的距离为L.现将物块A缓慢斜向上移动,直到弹簧刚恢复原长时的位置,并由静止释放物块A,当物块B刚要离开地面时,物块A的速度即变为零,求:在以后的运动过程中物块A最大速度的大小.