题目内容
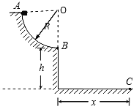
【题目】如图所示,在竖直平面内有一个粗糙的
圆弧轨道，其半径R=0.6m，轨道的最低点距地面高度h=0.8m，一质量m=0.2kg的小滑块从轨道的最高点A由静止释放，到达最低点B时以一定的水平速度离开轨道，落地点C距轨道最低点的水平距离x=1.2m，空气阻力不计，g取10m/s2求:
(1)小滑块离开轨道时的速度大小；
(2)小滑块运动到轨道最低点B时，对轨道的压力大小；
(3)从A到B，摩擦力对滑块所做的功。
【答案】（1）3.0m/s；（2）5N，方向竖直向下；（3）-0.3J
【解析】
（1）小滑块离开轨道后做平抛运动，设运动时间为t，初速度为v，
水平方向：x=vt，
竖直方向：
，
代入数据解得：v=3.0m/s；
（2）小滑块到达轨道最低点时，受重力和轨道对它的弹力为N，由牛顿第二定律得：
代入数据解得：N=5N，
根据牛顿第三定律，轨道受到的压力大小N'=N=5N，方向竖直向下；
（3）小滑块从A到B，设摩擦力做功为Wf，由动能定理得：mgR+Wf= 
代入数据解得：Wf=-0.3J
阳光课堂课时优化作业系列答案
【题目】一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系，进行了如下实验：在离地面高度为h的光滑水平桌面上，沿着与桌子边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的一个小钢球接触．当弹簧处于自然长度时，小钢球恰好在桌子边缘，如图所示．让钢球向左压缩弹簧一段距离后由静止释放，使钢球沿水平方向射出桌面，小钢球在空中飞行后落在水平地面上，水平距离为s．
（1）请你推导出弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式： Ep= ．
（2）弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如下表所示：
弹簧的压缩量x （cm） | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
小钢球飞行的水平距离s （cm） | 1.01 | 1.50 | 2.01 | 2.49 | 3.01 | 3.50 |
根据上面的实验数据，请你猜测弹簧的弹性势能Ep与弹簧的压缩量x之间的关系为
