题目内容
3.一辆巡逻车最快能在10s内由静止加速到最大速度40m/s,并能保持这个速度匀速行驶.在平直的高速公路上,该巡逻车由静止开始启动加速,追赶前方x0=2000m处正以32m/s的速度匀速行驶的一辆卡车,求:(1)巡逻车与卡车何时相距最远,最远距离是多少;
(2)巡逻车至少需要多少时间才能追上卡车?
分析 (1)当两车速度相等时,相距最远,结合运动学公式求出相距最远的距离.
(2)根据位移关系,结合运动学公式求出追及的时间.
解答 解:(1)根据v=at得,巡逻车加速度a=$\frac{40}{10}m/{s}^{2}$=4m/s2
当二者速度相等时相距最远,即v1=v2
代入数据有:4t=32
解得t=8s.
当t=8s时,x1=$\frac{1}{2}a{t^2}$=$\frac{1}{2}×4×64m$=128m
x2=vt=32×8m=256m
∴△x=x2-x1+x0=2128m.
(2)设经过时间t巡逻车追上卡车,即
x1=x0+x2
x1=$\frac{0+40}{2}10$+40(t-10)
x2=32t
解得t=275s
答:(1)巡逻车与卡车经过8s相距最远,最远距离是2128m;
(2)巡逻车至少需要275s时间才能追上卡车.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时,相距最远,注意巡逻车达到最大速度后做匀速直线运动.

练习册系列答案
相关题目
14.一列简谐横波沿x轴正方向传播,波速为v,位于x=0处的波源从平衡位置开始沿y轴正方向Z简谐运动,振动周期为T,质点P在x=2.5vT处,下列说法正确的是( )
| A. | 质点P振动周期为T,速度的最大值为v? | |
| B. | 若某时刻质点P的速度方向沿y轴负方向,则该时刻波源速度方向沿y轴正方向? | |
| C. | 质点P开始振动的方向沿y轴正方向? | |
| D. | 若某时刻波源在波峰,则质点P-定在波谷? | |
| E. | 若某时刻波源在波谷,则质点P-定在波谷 |
8. 如图所示,质量均为m的物体A、B通过一劲度系数为K的轻质弹簧相连,开始时B放在地面上,A.B都处于静止状态,现通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面.若将A加速向上拉起,B刚要离开地面时,A上升的距离为L2.假设弹簧一直在弹性限度内,则( )
如图所示,质量均为m的物体A、B通过一劲度系数为K的轻质弹簧相连,开始时B放在地面上,A.B都处于静止状态,现通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面.若将A加速向上拉起,B刚要离开地面时,A上升的距离为L2.假设弹簧一直在弹性限度内,则( )
 如图所示,质量均为m的物体A、B通过一劲度系数为K的轻质弹簧相连,开始时B放在地面上,A.B都处于静止状态,现通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面.若将A加速向上拉起,B刚要离开地面时,A上升的距离为L2.假设弹簧一直在弹性限度内,则( )
如图所示,质量均为m的物体A、B通过一劲度系数为K的轻质弹簧相连,开始时B放在地面上,A.B都处于静止状态,现通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面.若将A加速向上拉起,B刚要离开地面时,A上升的距离为L2.假设弹簧一直在弹性限度内,则( )| A. | L1=L2=$\frac{mg}{k}$ | B. | L1=L2=$\frac{2mg}{k}$ | C. | L1=$\frac{mg}{k}$,L2>L1 | D. | L1=$\frac{2mg}{k}$,L2>L1 |
15.物体以5m/s的初速度沿光滑斜面向上做匀变速直线运动,经4s后又滑回到原处时,速度大小仍为5m/s.则物体的加速度为( )
| A. | 2.5,方向沿斜面向下 | B. | 10,方向沿斜面向下 | ||
| C. | 5,方向沿斜面向下 | D. | 0 |
12.某放射性元素的原子核内有N个核子,其中有n个质子,该原子核发生2次α衰变和1次β衰变,变成1个新核,则( )
| A. | 衰变前原子核有n个中子 | |
| B. | 衰变前原子核有N-n个中子 | |
| C. | 衰变后新核有(n-3)个质子 | |
| D. | 衰变后新核的核子数为(N-3) | |
| E. | 衰变前原子核的质量数等于衰变后新核质量数与放出粒子质量数之和 |
 如图所示,在竖直平面内的平面直角坐标系xoy中,x轴上方有水平向右的匀强电场,有一质量为m,电荷量为-q(-q<0)的带电绝缘小球,从y轴上的P(0,L)点由静止开始释放,运动至x轴上的A(-L,0)点时,恰好无碰撞地沿切线方向进入在x轴下方竖直放置的四分之三圆弧形光滑绝缘细管.细管的圆心O1位于y轴上,交y轴于点B,交x轴于A点和C(L,0)点.该细管固定且紧贴x轴,内径略大于小球外径.小球直径远小于细管半径,不计一切阻力,重力加速度为g.求:
如图所示,在竖直平面内的平面直角坐标系xoy中,x轴上方有水平向右的匀强电场,有一质量为m,电荷量为-q(-q<0)的带电绝缘小球,从y轴上的P(0,L)点由静止开始释放,运动至x轴上的A(-L,0)点时,恰好无碰撞地沿切线方向进入在x轴下方竖直放置的四分之三圆弧形光滑绝缘细管.细管的圆心O1位于y轴上,交y轴于点B,交x轴于A点和C(L,0)点.该细管固定且紧贴x轴,内径略大于小球外径.小球直径远小于细管半径,不计一切阻力,重力加速度为g.求: 如图所示,在磁感应强度B=1T、方向竖直向下的匀强磁场中,有一个与水平面成θ=37°角的导电滑轨,滑轨上放置一个可自由移动的金属杆ab.已知接在滑轨中的电源电动势E=12V,内阻r=0.1Ω.ab杆长L=0.5m,质量m=0.2kg,棒的中点用细绳经定滑轮与一物体相连(绳与棒垂直,与轨道面平行),物体的质量为M=0.3kg.杆与滑轨间的动摩擦因数μ=0.1,滑轨与ab杆的电阻忽略不计.求:要使ab杆在滑轨上保持静止,滑动变阻器R的阻值在什么范围内变化?(g取10m/s2,sin 37°=0.6,cos 37°=0.8,可认为最大静摩擦力等于滑动摩擦力,结果保留两位有效数字)
如图所示,在磁感应强度B=1T、方向竖直向下的匀强磁场中,有一个与水平面成θ=37°角的导电滑轨,滑轨上放置一个可自由移动的金属杆ab.已知接在滑轨中的电源电动势E=12V,内阻r=0.1Ω.ab杆长L=0.5m,质量m=0.2kg,棒的中点用细绳经定滑轮与一物体相连(绳与棒垂直,与轨道面平行),物体的质量为M=0.3kg.杆与滑轨间的动摩擦因数μ=0.1,滑轨与ab杆的电阻忽略不计.求:要使ab杆在滑轨上保持静止,滑动变阻器R的阻值在什么范围内变化?(g取10m/s2,sin 37°=0.6,cos 37°=0.8,可认为最大静摩擦力等于滑动摩擦力,结果保留两位有效数字)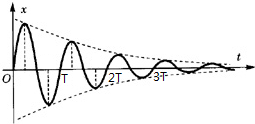 弹簧振子可以作简谐振动,考虑阻力存在,振子振动过程中能量不断损失,这种振动称阻尼振动.现通过实验手段得到某振子阻尼振动的图象和经理论推导得到阻尼振动的周期公式T2=$\frac{2π}{({ω}_{0}^{2}-β)^{\frac{1}{2}}}$${\;}^{\frac{1}{2}}$,(ω0为该振子无阻尼时的角速度,β为阻尼系数、对某次阻尼振动β为常数)审题后指出阻尼振动的特点振幅逐渐减小、周期不变(写出两点)
弹簧振子可以作简谐振动,考虑阻力存在,振子振动过程中能量不断损失,这种振动称阻尼振动.现通过实验手段得到某振子阻尼振动的图象和经理论推导得到阻尼振动的周期公式T2=$\frac{2π}{({ω}_{0}^{2}-β)^{\frac{1}{2}}}$${\;}^{\frac{1}{2}}$,(ω0为该振子无阻尼时的角速度,β为阻尼系数、对某次阻尼振动β为常数)审题后指出阻尼振动的特点振幅逐渐减小、周期不变(写出两点)