题目内容
9.探究重物下落过程中动能与重力势能相互转化机械能守恒问题的实验.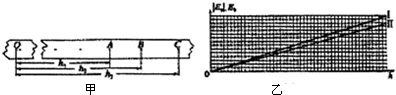
(1)部分实验操作步骤如下,请将步骤B补充完整.
A.按实验要求安装好实验装置;
B.使重物靠近打点计时器下端,接着先接通电源,后释放纸带,打点计时器在纸带上打下一系列的点.
(2)图甲是一条符合实验要求的纸带,O点为打点计时器打下的第一点.分别测出若干连续点A、B、C…与O点的距离h1、h2、h3…已知打点计时器的打点周期为T,重物质量为m,重力加速度为g,可得重物下落到B点的过程中,重物增加的动能为$\frac{m({h}_{3}-{h}_{1})^{2}}{8{T}^{2}}$,减少的重力势能为mgh2.
(3)取打下O点时重物的重力势能为零,计算出该重物下落不同高度h时所对应的动能EK和重力势能的绝对值|EP|,建立坐标系,横轴表示h,纵轴表示|EP|和EK,根据以上数据在图乙中分别绘出对应的图线I(|EP|~h)和图线Ⅱ(EK~h),图线Ⅰ、Ⅱ的斜率分别为忌k1、k2.
A.图线Ⅰ和图线Ⅱ不重合的主要原因是重物下落过程克服阻力做功.
B.重物和纸带下落过程中所受平均阻力与重物所受重力的比值为$\frac{{K}_{1}-{K}_{2}}{{K}_{1}}$(用k1、k2表示).
分析 (1)实验时为了提高纸带的利用率,应先接通电源后释放纸带;
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的速度,从而得出动能的增加量,根据下降的高度求出重力势能的减小量.
(3)若机械能守恒,因为初位置的机械能为零,则每个位置动能和重力势能的绝对值应该相等,图线不重合的原因是重物和纸带下落过程中需克服阻力做功.根据动能定理,结合图线的斜率求出阻力与重物重力的比值.
解答 解:(1)如果先释放纸带后接通电源,有可能会出现小车已经拖动纸带运动一段距离,电源才被接通,那么纸带上只有很小的一段能打上点,大部分纸带没有打上点,纸带的利用率太低;所以应当先接通电源,后让纸带运动.
(2)B点的瞬时速度vB=$\frac{{h}_{3}-{h}_{1}}{2T}$,则重物动能的增加量△Ek=$\frac{1}{2}$mvB2=$\frac{m({h}_{3}-{h}_{1})^{2}}{8{T}^{2}}$,重力势能的减小量为△Ep=mgh2.
(3)取打下O点时重物的重力势能为零,因为初位置的动能为零,则机械能为零,每个位置对应的重力势能和动能互为相反数,即重力势能的绝对值与动能相等,而图线的斜率不同,原因是重物和纸带下落过程中需要克服阻力做功.
根据动能定理得,mgh-fh=$\frac{1}{2}$mv2,则mg-f=$\frac{m{v}^{2}}{2h}$,图线斜率k1=$\frac{mgh}{h}$=mg,
图线斜率k2=$\frac{m{v}^{2}}{2h}$,知k1-f=k2,则阻力f=k1-k2.
所以重物和纸带下落过程中所受平均阻力与重物所受重力的比值为$\frac{{k}_{1}-{k}_{2}}{{k}_{1}}$.
故答案为:①先接通电源后释放纸带;②$\frac{m({h}_{3}-{h}_{1})^{2}}{8{T}^{2}}$,mgh2;
③重物和纸带下落过程中需要克服阻力做功,$\frac{{k}_{1}-{k}_{2}}{{k}_{1}}$.
点评 解决本题的关键知道实验的原理,验证重力势能的减小量与动能的增加量是否相等.以及知道通过求某段时间内的平均速度表示瞬时速度.

 名校课堂系列答案
名校课堂系列答案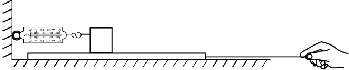
| A. | 拉木板的拉力等于弹簧测力计示数 | |
| B. | 拉木板的拉力小于弹簧测力计示数 | |
| C. | 拉木板的拉力大于弹簧测力计示数 | |
| D. | 拉木板的拉力小于、等于、大于弹簧测力计示数均可 |
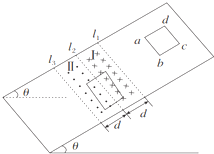 如图所示,在倾斜角为θ的光滑斜面上,相距均为d的三条虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框从l1上方一定高度处由静止开始沿斜面下滑,当ab边在越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )
如图所示,在倾斜角为θ的光滑斜面上,相距均为d的三条虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框从l1上方一定高度处由静止开始沿斜面下滑,当ab边在越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )| A. | 线框中感应电流的方向不变 | |
| B. | 线框ab边从l1运动到l2所用时间大于从l2运动到l3所用时间 | |
| C. | 线框以速度v2匀速直线运动时,发热功率为$\frac{{m}^{2}{g}^{2}Rsi{n}^{2}θ}{4{B}^{2}{d}^{2}}$ | |
| D. | 线框从ab边进入磁场到速度变为v2的过程中,减少的机械能△E机与重力做功WG的关系式是△E机=WG+$\frac{1}{2}$mv${\;}_{1}^{2}$-$\frac{1}{2}$mv${\;}_{2}^{2}$ |
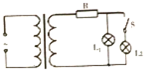 如图所示,理想变压器原、副线圈的匝数比为10:1,原线圈接电压恒定的交流电,副线圈输出端接有R=4Ω的电阻和两个“18V,9W”相同小灯泡,当开关S断开时,小灯泡L1刚好正常发光,则( )
如图所示,理想变压器原、副线圈的匝数比为10:1,原线圈接电压恒定的交流电,副线圈输出端接有R=4Ω的电阻和两个“18V,9W”相同小灯泡,当开关S断开时,小灯泡L1刚好正常发光,则( )| A. | 原线圈输入电压为20V | |
| B. | S断开时,原线圈中的电流为0.5A | |
| C. | 闭合开关S后,原、副线圈中的电流之比增大 | |
| D. | 闭合开关S后,小灯泡L1消耗的功率减小 |
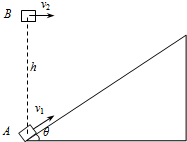 如图所示,在水平地面上固定一倾角θ=37°的长斜面体,物体A以v1=8m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出.物体A上滑过程中速度减小,当速度减为零时恰好被B物体击中.已知物体A与斜面体间的动摩擦因数为0.25.(A、B均可看作质点,sin37°=0.6,cos37°=0.8,g取10m/s2)求:
如图所示,在水平地面上固定一倾角θ=37°的长斜面体,物体A以v1=8m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出.物体A上滑过程中速度减小,当速度减为零时恰好被B物体击中.已知物体A与斜面体间的动摩擦因数为0.25.(A、B均可看作质点,sin37°=0.6,cos37°=0.8,g取10m/s2)求: 如图所示,是一物体在距某一行星表面附近某一高度处的O点,由静止开始做自由落体运动的闪光照片,其频闪频率为10Hz,图中A、B、C、D是连续的四个点,其中,AC段与CD段的距离相等,均为0.24m,若该星球的半径为180km,则:
如图所示,是一物体在距某一行星表面附近某一高度处的O点,由静止开始做自由落体运动的闪光照片,其频闪频率为10Hz,图中A、B、C、D是连续的四个点,其中,AC段与CD段的距离相等,均为0.24m,若该星球的半径为180km,则: MNPQ是边长为30cm的正方形玻璃砖.利用插针法测它的折射率,大头针P1、P2、P3、P4位置如图.已知B为MQ中点,DP=7.5cm,α角等于30°,取sin37°=0.6,cos37°=0.8,求玻璃砖的折射率.
MNPQ是边长为30cm的正方形玻璃砖.利用插针法测它的折射率,大头针P1、P2、P3、P4位置如图.已知B为MQ中点,DP=7.5cm,α角等于30°,取sin37°=0.6,cos37°=0.8,求玻璃砖的折射率.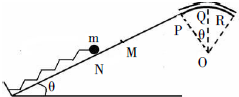 如图所示,在倾角为θ=37°的斜面底端固定有一轻质弹簧,自由放置时其上端位于M点,M点距斜面最高点P的距离L=2m.把质量为m=1kg的小球放于M点,通过外力控制小球将弹簧压缩至N点后自由释放(小球与弹簧不相连,其中MN 的距离d=0.5m),小球通过M点后上升过程中位移随时间变化的关系为x=6t-4t2,之后小球从P点沿切线进入竖直放置的光滑圆弧形圆管轨道运动,圆弧轨道半径R=0.4m,圆管内径可忽略不计(sin37°=0.6,cos37°=0.8,g=10m/s2). 求:
如图所示,在倾角为θ=37°的斜面底端固定有一轻质弹簧,自由放置时其上端位于M点,M点距斜面最高点P的距离L=2m.把质量为m=1kg的小球放于M点,通过外力控制小球将弹簧压缩至N点后自由释放(小球与弹簧不相连,其中MN 的距离d=0.5m),小球通过M点后上升过程中位移随时间变化的关系为x=6t-4t2,之后小球从P点沿切线进入竖直放置的光滑圆弧形圆管轨道运动,圆弧轨道半径R=0.4m,圆管内径可忽略不计(sin37°=0.6,cos37°=0.8,g=10m/s2). 求: