题目内容
如图5所示,木块A和B用一轻质弹簧相连,竖直放在木块C上,三者静置于地面,它们的质量之比是1∶2∶3.设所有接触面都光滑,当沿水平方向迅速抽出木块C的瞬间,求A和B的加速度.

见分析
【试题分析】
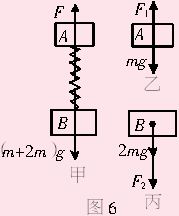
对A和B整体,在抽出木块C的瞬间前处于静止状态,受力如图6甲,有
F-(m+2m)g=0
解得F=3mg,方向竖直向上;
对A,在抽出木块C的瞬间,受力如图6乙,由于弹簧形变明显,恢复需要较长时间,认为在瞬间弹簧保持原来形变,则有与抽出木块C的瞬间前相同的竖直向上弹力F1,仍处于静止状态其加速度a1=0.
对B,在抽出木块C的瞬间,与抽出木块C的瞬间前相比,少了竖直向上的弹力F,其他力不变,受力如图6丙,重力和弹力提供合外力,方向竖直向下,合力大小等于F,根据牛顿第二定律得
a2=F/2m
=3mg/2m=1.5g,方向竖直向下.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
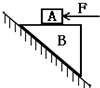 如图所示,木块A和B接触面水平,在水平力作用下(F≠0),木块A、B 保持静止,则木块B受力的个数可能是( )
如图所示,木块A和B接触面水平,在水平力作用下(F≠0),木块A、B 保持静止,则木块B受力的个数可能是( )


 B.
B.
 D.
D.
 和M固定在轻质弹簧的两端,静止于光滑的水平面上.一质量为M/4的木块A以速度v水平向右与木块B对心碰撞,并粘在一起运动,求弹簧的最大弹性势能Em.
和M固定在轻质弹簧的两端,静止于光滑的水平面上.一质量为M/4的木块A以速度v水平向右与木块B对心碰撞,并粘在一起运动,求弹簧的最大弹性势能Em.