题目内容
甲、乙两小孩在平直跑道上做游戏,分别将质量为m﹦10kg的物体从同一起跑线沿直线推到距离起跑线x﹦18m的P点.其中甲用水平F1﹦50N持续作用在物体上,在t1﹦3s末物体运动到P点.(1)小孩乙也用水平力推该物体,要使物体也能到达P点,则至少要对物体做多少功;(2)小孩乙用F2﹦30N的水平推力作用t2﹦5s就撤去,物体停止运功时距离起跑线多远.
分析:(1)根据位移时间公式求出物体的加速度,结合牛顿第二定律摩擦力的大小,再通过动能定理分析,小孩乙至少做功的多少.
(2)根据牛顿第二定律求出小孩乙推物体的加速度,从而得出匀加速直线运动的位移,再结合牛顿第二定律求出撤去拉力后的加速度,结合速度位移公式求出匀减速直线运动的位移,从而确定物体停止运动时距离起跑线的距离.
(2)根据牛顿第二定律求出小孩乙推物体的加速度,从而得出匀加速直线运动的位移,再结合牛顿第二定律求出撤去拉力后的加速度,结合速度位移公式求出匀减速直线运动的位移,从而确定物体停止运动时距离起跑线的距离.
解答:解:(1)根据x=
a1t12得,a1=
=
m/s2=4m/s2.
根据牛顿第二定律得,F1-f=ma1,解得f=F1-ma1=50-10×4N=10N.
设乙至少做功为W,根据动能定理得,
W-fx=0.
解得W=fx=10×18J=180J.
(2)根据牛顿第二定律得,a2=
=
m/s2=2m/s2.
则5s内的位移x1=
a2t2=
×2×25m=25m
5s末的速度v=a2t=2×5m/s=10m/s.
匀减速运动的加速度a3=
=1m/s2.
则匀减速直线运动的位移x2=
=
m=50m.
则s=x1+x2=75m.
答:(1)至少要对物体做功180J.
(2)物体停止运功时距离起跑线75m.
| 1 |
| 2 |
| 2x |
| t12 |
| 2×18 |
| 9 |
根据牛顿第二定律得,F1-f=ma1,解得f=F1-ma1=50-10×4N=10N.
设乙至少做功为W,根据动能定理得,
W-fx=0.
解得W=fx=10×18J=180J.
(2)根据牛顿第二定律得,a2=
| F2-f |
| m |
| 30-10 |
| 10 |
则5s内的位移x1=
| 1 |
| 2 |
| 1 |
| 2 |
5s末的速度v=a2t=2×5m/s=10m/s.
匀减速运动的加速度a3=
| f |
| m |
则匀减速直线运动的位移x2=
| v2 |
| 2a3 |
| 100 |
| 2 |
则s=x1+x2=75m.
答:(1)至少要对物体做功180J.
(2)物体停止运功时距离起跑线75m.
点评:本题可以运用动能定理求解,也可以通过动力学至少求解,动能定理解题的优越性在于不考虑运动的过程,抓住初末状态进行求解.

练习册系列答案
相关题目
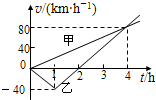 (2011?龙岩模拟)甲、乙两汽车在平直公路上从同一地点同时开始行驶,它们的v-t图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )
(2011?龙岩模拟)甲、乙两汽车在平直公路上从同一地点同时开始行驶,它们的v-t图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( ) 如图,甲、乙两同学在直跑道上练习4×100m接力,他们在奔跑时具有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在,甲持棒以最大速度向乙匀速奔跑,乙在接力区待机全力奔出.若要求乙接棒时的速度达到最大速度的80%,则乙应在距离甲多远处起跑.
如图,甲、乙两同学在直跑道上练习4×100m接力,他们在奔跑时具有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在,甲持棒以最大速度向乙匀速奔跑,乙在接力区待机全力奔出.若要求乙接棒时的速度达到最大速度的80%,则乙应在距离甲多远处起跑.