题目内容
20.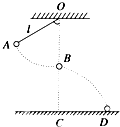 如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时线被拉断.设摆线长l=1.6m,摆球质量为0.5kg,摆线的最大拉力为10N,悬点与地面的竖直高度为H=4.8m,不计空气阻力,g=10m/s2.求:
如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时线被拉断.设摆线长l=1.6m,摆球质量为0.5kg,摆线的最大拉力为10N,悬点与地面的竖直高度为H=4.8m,不计空气阻力,g=10m/s2.求:(1)摆球在B点速度大小;
(2)D点到C点的距离.
分析 (1)摆球摆到最低点B位置时,由重力和细线的拉力提供小球的向心力,根据牛顿第二定律求解小球经过B点时的速度大小.
(2)细线被拉断后,摆球做平抛运动,平抛运动的高度为h=H-l=3.2mm,由求出时间H-l=$\frac{1}{2}g{t}^{2}$,运用运动的分解方法求出平抛运动的水平距离DC.
解答 解:(1)小球刚摆到B点时,由牛顿第二定律可知
Fm-mg=m$\frac{{v}_{B}^{2}}{l}$ ①
由①并代入数据可解得:
vB=$\sqrt{\frac{l({F}_{m}-mg)}{m}}$=$\sqrt{\frac{1.6×(10-0.5×10)}{0.5}}$m/s=4m/s ②
(2)小球离过B后,作平抛运动,竖直方向;H-l=$\frac{1}{2}g{t}^{2}$ ③
落地点D到C的距离
S=vBt
代入数据解得:s=3.2m
答:(1)摆球在B点速度大小是4m/s;(2)落地点D到C点的距离为3.2m.
点评 本题是圆周运动与平抛运动的综合,采用程序法分析求解.两个过程机械能都守恒.属于基础题.

练习册系列答案
相关题目
11.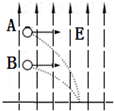 如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )
如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )
 如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )
如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )| A. | 它们下落的时间tA>tB | |
| B. | 如果是A球带电,则A球带正电 | |
| C. | 如果是A球带电,A球下落时电势能减少 | |
| D. | 如果是B球带电,则B球只能带正电 |
8.如图,A、B是相同的白炽灯,L是自感系数很大、电阻可忽略的自感线圈.下面说法正确的是( )


| A. | 闭合开关S时,A、B灯同时亮,且达到正常 | |
| B. | 闭合开关S时,B灯比A灯先亮,最后一样亮 | |
| C. | 闭合开关S时,A灯比B灯先亮,最后A灯比B灯更亮 | |
| D. | 断开开关S时,A灯与B灯同时慢慢熄灭 |
15.下列说法中符合开普勒对行星绕太阳运动的描述是( )
| A. | 所有的行星绕太阳作匀速圆周运动 | |
| B. | 行星绕太阳运动的轨迹是椭圆,太阳在椭圆的一个焦点上 | |
| C. | 行星从近日点向远日点运动时,速率逐渐增大 | |
| D. | 离太阳越远的行星,公转周期越短 |
5.在宇宙发展演化的理论中,有一种学说叫“宇宙膨胀说”,就是天体的距离在不断增大,根据这一理论,在很久很久以前,太阳系中地球的公转情况与现在相比( )
| A. | 公转半径较大 | B. | 公转周期较小 | C. | 公转周期较大 | D. | 公转角速度较大 |
12. 从表中选出适当器材,设计一电路来测量一个刻度盘总共有10个小格且刻度均匀、但量程未准确确定的电压表V1的量程U1m,要求方法简捷,有尽可能高的准确度,并能测出多组数据.
从表中选出适当器材,设计一电路来测量一个刻度盘总共有10个小格且刻度均匀、但量程未准确确定的电压表V1的量程U1m,要求方法简捷,有尽可能高的准确度,并能测出多组数据.
①画出电路,标明所用器材的代号;
②若选用测量数据中的一组合理数据来计算V1的量程U1m,则表达式U1m=$\frac{10{U}_{2}{r}_{1}}{n{r}_{2}}$,式中各字母代表的是U2为电压表V2的读数,n为此次测量V1表的指针偏转格数,r1、r2分别为V1、V2表的内电阻..
 从表中选出适当器材,设计一电路来测量一个刻度盘总共有10个小格且刻度均匀、但量程未准确确定的电压表V1的量程U1m,要求方法简捷,有尽可能高的准确度,并能测出多组数据.
从表中选出适当器材,设计一电路来测量一个刻度盘总共有10个小格且刻度均匀、但量程未准确确定的电压表V1的量程U1m,要求方法简捷,有尽可能高的准确度,并能测出多组数据.| 器材(代号) | 规 格 |
| 待测电压表V1 | 量程约25V,内阻r1=250kΩ |
| 标准电压表V2 | 量程2V,内阻r2=20kΩ |
| 电流表A | 量程3A,内阻r3=0.01Ω |
| 滑动变阻器R | 总阻值1kΩ |
| 稳压电源E | 30V,内阻很小 |
| 开关S | |
| 导线若干 |
②若选用测量数据中的一组合理数据来计算V1的量程U1m,则表达式U1m=$\frac{10{U}_{2}{r}_{1}}{n{r}_{2}}$,式中各字母代表的是U2为电压表V2的读数,n为此次测量V1表的指针偏转格数,r1、r2分别为V1、V2表的内电阻..
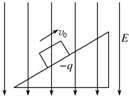 如图所示,绝缘斜面固定在水平地面上,斜面所在空间存在竖直向下的匀强电场.一带负电荷的滑块以初速度v0沿斜面上滑.已知滑块始终在斜面上运动,下面四个图象分别表示滑块运动过程中的速度-时间图象,其中可能正确的是( )
如图所示,绝缘斜面固定在水平地面上,斜面所在空间存在竖直向下的匀强电场.一带负电荷的滑块以初速度v0沿斜面上滑.已知滑块始终在斜面上运动,下面四个图象分别表示滑块运动过程中的速度-时间图象,其中可能正确的是( )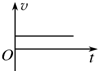

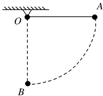 如图,小球质量为m,一不可伸长的悬线长为l,把悬线拉到水平位置后释放,小球在最低点所受拉力为F,不计空气阻力,则小球从水平位置A到竖直位置B的过程中,
如图,小球质量为m,一不可伸长的悬线长为l,把悬线拉到水平位置后释放,小球在最低点所受拉力为F,不计空气阻力,则小球从水平位置A到竖直位置B的过程中,