题目内容
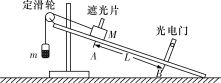
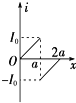
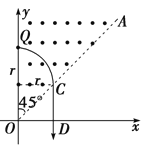
【题目】如图所示,一面积为S的单匝圆形金属线圈,线圈内存在一个方向垂直纸面向里、磁感应强度大小均匀增加且变化率为k的磁场Bt。平行金属板M、N,两板间距为d,N板右侧xOy坐标系(坐标原点O在N板的下端)的第一象限内,有垂直纸面向外的匀强磁场,磁场边界OA和y轴的夹角∠AOy=45°,AOx区域为无场区。在靠近M板处的P点由静止释放一质量为m、带电荷量为+q的粒子(不计重力),经过N板的小孔,从点Q(0,l)垂直y轴进入第一象限,经OA上某点离开磁场,最后垂直x轴离开第一象限。求:

(1)平行金属板M、N获得的电压U;
(2)yOA区域内匀强磁场的磁感应强度B;
(3)粒子从P点射出至到达x轴的时间。
【答案】(1)kS(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)根据法拉第电磁感应定律,知感应电动势为![]() ①
①
(2)因平行金属板M,N与电阻并联,故M、N两板间的电压为U=E=kS②
带电粒子在M、N间做匀加速直线运动,有
qU=![]() mv2③
mv2③
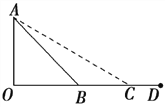
带电粒子进入磁场区域的运动轨迹如图所示,
有qvB=m![]() ④
④
由几何关系可得r+rcot45°=l⑤
联立②③④⑤得![]() 。
。
(3)粒子在电场中,有d=![]() at12
at12
q![]() =ma
=ma
粒子在磁场中,有![]()
t2=![]() T
T
粒子在第一象限的无场区中,有s=vt3
由几何关系得s=r
粒子从P点射出至到达x轴的时间为t=t1+t2+t3
联立以上各式可得![]() 。
。

练习册系列答案
相关题目