题目内容
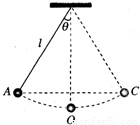如图所示，把一个小球用细线悬挂起来，就成为一个摆，摆长为l，最大偏角为θ．如果阻力可以忽略，（1）小球运动到最低位置时的速度是多大？
（2）在最低点，细线的拉力为多大？
【答案】分析：小球在摆动的过程中，只有重力做功，机械能守恒，根据机械能守恒定律求出小球运动到最低位置时的速度大小．在最低点，小球靠重力和拉力的合力提供向心力，根据牛顿第二定律求出细线的拉力大小．
解答：解（1）由最大偏角θ处下落，到最低点时，竖直的高度差是h=l（1-cosθ）
有机械能守恒定律知
所以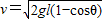
（2）在最低点合外力提供向心力
解得F拉=3mg-2mgcosθ
答：（1）小球运动到最低位置时的速度是
．
（2）在最低点，细线的拉力为3mg-2mgcosθ．
点评：本题综合考查了机械能守恒定律和牛顿第二定律，难度不大，需加强这方面的训练，基础题．
解答：解（1）由最大偏角θ处下落，到最低点时，竖直的高度差是h=l（1-cosθ）
有机械能守恒定律知
所以
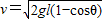
（2）在最低点合外力提供向心力
解得F拉=3mg-2mgcosθ
答：（1）小球运动到最低位置时的速度是
．（2）在最低点，细线的拉力为3mg-2mgcosθ．
点评：本题综合考查了机械能守恒定律和牛顿第二定律，难度不大，需加强这方面的训练，基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，把一个小球用细线悬挂起来，就成为一个摆，摆长为l，最大偏角为θ．如果阻力可以忽略，
如图所示，把一个小球放在玻璃漏斗中，晃动漏斗，可以使小球沿光滑的漏斗壁在某一水平面内做匀速圆周运动．小球的向心力由以下哪个力提供（ ）
