题目内容
【题目】如图所示，M是水平放置的半径足够大的圆盘，可绕过其圆心的竖直轴OO′匀速转动，在圆心O正上方h处有一个正在间断滴水的容器，每当一滴水落在盘面时恰好下一滴水离开滴口．某次一滴水离开滴口时，容器恰好开始水平向右做速度为v的匀速直线运动，将此滴水记作第一滴水．不计空气阻力，重力加速度为g．求：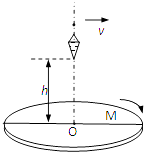
（1）相邻两滴水下落的时间间隔；
（2）要使每一滴水在盘面上的落点都在一条直线上，求圆盘转动的角速度；
（3）第二滴和第三滴水在盘面上落点之间的距离最大可为多少？
【答案】
（1）
解：相邻两滴水离开滴口的时间间隔就是一滴水下落的时间
由h= 
g△t2，
可得△t= 
（2）
解：每一滴水在盘面上的落点都在一条直线上，△t时间内圆盘转过的弧度为kπ
ω= 
= 
=kπ 
，k=1，2…
（3）
解：第二滴和第三滴水的落点恰能在一条直径上且位于O点两侧时，距离最大
s1=v2△t…（1分），s2=v3△t
所以s=s1+s2=v2△t+v3△t
s=5v
【解析】（1）水滴滴下做自由落体运动，根据h= gt2可求时间间隔；（2）水滴滴下后做平抛运动，根据高度求出时间．根据圆周运动的周期性，可分析得出使每一滴水在盘面上的落点都位于一条直线上的条件，求出角速度；（3）当第二滴水与第三滴水在盘面上的落点位于同一直径上圆心的两侧时两点间的距离最大．利用水平间关系关系可求出．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
