题目内容
15. 如图所示,离地面高h处有甲、乙两个物体,甲以初速度v0水平射出,同时乙以初速度v0沿倾角为30°的光滑斜面滑下.若甲到达地面的同时乙恰好运动到斜面的中点处,则v0的大小是( )
如图所示,离地面高h处有甲、乙两个物体,甲以初速度v0水平射出,同时乙以初速度v0沿倾角为30°的光滑斜面滑下.若甲到达地面的同时乙恰好运动到斜面的中点处,则v0的大小是( )| A. | $\frac{\sqrt{2gh}}{2}$ | B. | $\frac{\sqrt{gh}}{4}$ | C. | $\frac{\sqrt{2gh}}{4}$ | D. | $\sqrt{2gh}$ |
分析 平抛运动的时间由高度决定,结合高度求出平抛运动的时间,根据斜面的长度,结合牛顿第二定律求出加速度,根据位移时间公式,抓住时间相等求出v0的大小.
解答 解:甲平抛运动的时间为:t=$\sqrt{\frac{2h}{g}}$;
乙在斜面下滑的加速度为:a=$\frac{mgsin30°}{m}$=0.5g.
对于乙,下滑的位移大小为 h.
根据 h=v0t+$\frac{1}{2}$at2,代入数据得:
解得 v0=$\frac{\sqrt{2gh}}{4}$
故选:C.
点评 解决本题的关键知道平抛运动的时间由高度决定,初速度和时间相同决定水平位移,抓住平抛运动的时间和匀加速运动的时间相同,结合牛顿第二定律和运动学公式灵活求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )
如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )
 如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )
如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )| A. | 缆绳拉力F1和拉绳拉力F2都增大 | |
| B. | 缆绳拉力F1和拉绳拉力F2都不变 | |
| C. | 缆绳与竖直方向的夹角α可能大于角β | |
| D. | 缆绳拉力F1的功率保持不变 |
7.下列关于动量的说法,正确的是( )
| A. | 质量大的物体,动量一定大 | |
| B. | 质量和速率都相同的物体,动量一定相同 | |
| C. | 一个物体的速率改变,它的动量一定改变 | |
| D. | 一个物体的运动状态改变,它的动量不一定改变 |
4.下列关于做匀速圆周运动的物体所受的向心力的说法中,正确的是( )
| A. | 物体除受到其他的力外还要受到一个向心力 | |
| B. | 物体所受的合外力提供向心力 | |
| C. | 向心力是一个恒力 | |
| D. | 向心力的大小一直不变 |
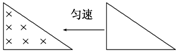 如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )
如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )



 物体A的质量m1=1kg,静止在光滑的水平面上的木板B的质量m2=0.5kg、长L=1m,A与B之间的动摩擦因数μ=0.2.某时刻A以v0=4m/s的初速度滑上木板B的上表面,从木板的另一端滑下.(重力加速度g取10m/s2)
物体A的质量m1=1kg,静止在光滑的水平面上的木板B的质量m2=0.5kg、长L=1m,A与B之间的动摩擦因数μ=0.2.某时刻A以v0=4m/s的初速度滑上木板B的上表面,从木板的另一端滑下.(重力加速度g取10m/s2) 如图所示质量为1kg的滑块从半径为50cm的半圆形轨道的边缘A点滑向底端B,此过程中,摩擦力做功为-3J.若滑块与轨道间的动摩擦因数为0.2,则在B点时滑块受到摩擦力的大小为(重力加速度g取10m/S2)( )
如图所示质量为1kg的滑块从半径为50cm的半圆形轨道的边缘A点滑向底端B,此过程中,摩擦力做功为-3J.若滑块与轨道间的动摩擦因数为0.2,则在B点时滑块受到摩擦力的大小为(重力加速度g取10m/S2)( )