题目内容
20.从某高度处以12m/s的初速度水平抛出一物体,落地时,物体水平射程是24m.则物体的抛出点高度是多少,落地时速度偏向角正切值是多少?分析 根据水平射程和初速度求出平抛运动的时间,结合位移时间公式求出抛出点的高度.根据平行四边形定则求出落地的速度方向与水平方向的夹角.
解答 解:物体平抛运动的时间t=$\frac{s}{{v}_{0}}=\frac{24}{12}s=2s$,
则下落的高度$h=\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×4m=20m$.
物体落地的竖直分速度vy=gt=10×2m/s=20m/s,
根据平行四边形定则知,tanθ=$\frac{{v}_{y}}{{v}_{0}}=\frac{20}{12}=\frac{5}{3}$.
答:物体的抛出点高度为20m,落地时速度偏向角正切值为$\frac{5}{3}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
8.如图所示是原子核的核子平均质量与原子序数z的关系图象,下列说法中正确的是( ) 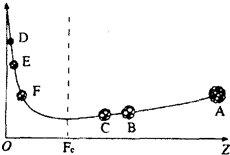

| A. | 若D和E结合成F,则有一部分质量转化为能量 | |
| B. | 若A能分裂成B和C,分裂过程一定要释放能量 | |
| C. | 在太阳内的核反应为A分裂成B和C的反应 | |
| D. | 若A能分裂成B和C,一个可能的方程为${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+2${\;}_{0}^{1}$n |
5.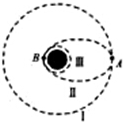 按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成,假设月球半径为R,月球表面的重力加速度为g0( )
按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成,假设月球半径为R,月球表面的重力加速度为g0( )
 按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成,假设月球半径为R,月球表面的重力加速度为g0( )
按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成,假设月球半径为R,月球表面的重力加速度为g0( )| A. | 飞船在轨道Ⅰ上的运动速率v=$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在A点点火变轨的瞬间,动能增加 | |
| C. | 飞船在A点的线速度大于在B点的线速度 | |
| D. | 飞船在轨道Ⅲ绕月球运动一周的时间为 2π$\sqrt{\frac{R}{{g}_{0}}}$ |
12.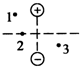 在等量异号电荷所在的平面上,先作两点电荷的连线,再作出该连线的中垂线,该平面上有1、2、3三个点,其中2点位于中垂线上,如图所示,三点电势高低关系为( )
在等量异号电荷所在的平面上,先作两点电荷的连线,再作出该连线的中垂线,该平面上有1、2、3三个点,其中2点位于中垂线上,如图所示,三点电势高低关系为( )
 在等量异号电荷所在的平面上,先作两点电荷的连线,再作出该连线的中垂线,该平面上有1、2、3三个点,其中2点位于中垂线上,如图所示,三点电势高低关系为( )
在等量异号电荷所在的平面上,先作两点电荷的连线,再作出该连线的中垂线,该平面上有1、2、3三个点,其中2点位于中垂线上,如图所示,三点电势高低关系为( )| A. | φ1>φ2>φ3 | B. | φ2>φ3>φ1 | C. | φ2>φ1>φ3 | D. | φ3>φ2>φ1 |
9.用伏安法测电阻时有如图所示的甲、乙两种接法,下面说法中正确的是( )


| A. | 甲电路和乙电路的测量结果都偏小 | |
| B. | 甲电路的测量结果总是偏大,乙电路的测量结果总是偏小 | |
| C. | 当Rx>>Rv时,用甲种接法误差较小,当Rx<<RA时,用乙种接法误差较小 | |
| D. | 当Rx<<RA时,用甲种接法误差较小,当Rx>>RV时,用乙种接法误差较小 |
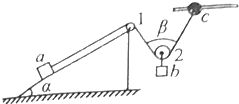 质量为5.4kg且倾角为α=37°的粗糙斜劈放置在水平面上,其与水平面间的动摩擦因数μ1=0.4,质量为5kg的物体a放在斜面上且与斜面间的动摩擦因数μ2=0.5.一根平行于斜面的轻质细线一端固定在物体a上,另一端绕过两个光滑小滑轮固定在水平横杆c处,滑轮2下吊有一物体b且β=74°,物体a受到斜劈的摩擦力大小为Ff,且最大静摩擦力等于滑动摩擦力,g取10N/kg,sin37°=0.6,cos37°=0.8.求:
质量为5.4kg且倾角为α=37°的粗糙斜劈放置在水平面上,其与水平面间的动摩擦因数μ1=0.4,质量为5kg的物体a放在斜面上且与斜面间的动摩擦因数μ2=0.5.一根平行于斜面的轻质细线一端固定在物体a上,另一端绕过两个光滑小滑轮固定在水平横杆c处,滑轮2下吊有一物体b且β=74°,物体a受到斜劈的摩擦力大小为Ff,且最大静摩擦力等于滑动摩擦力,g取10N/kg,sin37°=0.6,cos37°=0.8.求: 如图所示,一根长度为2L、质量为m的绳子挂在定滑轮的两侧,左右两边绳子的长度相等.绳子的质量分布均匀,滑轮的质量和大小均忽略不计,不计一切摩擦.由于轻微扰动,右侧绳从静止开始竖直下降,当它向下运动的位移为x时,加速度大小为a,滑轮对天花板的拉力为T.已知重力加速度大小为g,下列a-x、T-x关系图线正确的是( )
如图所示,一根长度为2L、质量为m的绳子挂在定滑轮的两侧,左右两边绳子的长度相等.绳子的质量分布均匀,滑轮的质量和大小均忽略不计,不计一切摩擦.由于轻微扰动,右侧绳从静止开始竖直下降,当它向下运动的位移为x时,加速度大小为a,滑轮对天花板的拉力为T.已知重力加速度大小为g,下列a-x、T-x关系图线正确的是( )