题目内容
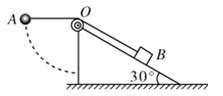
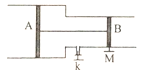
【题目】如图所示,两端开口的一导热性能良好的容器水平放置,两端是直径不同的两个圆筒,里面各有一个活塞,其横截面积分别为SA=10cm2和SB=10cm2,质量分别为MA=6kg、M=4kg。它们之间用一质量不计的轻质细杆相连,两活塞可在桶内无摩擦滑动,但不漏气。在气温为-23°时,用销子把B锁住,并把阀门k打开,使容器和大气相通,随后关闭阀门k,此时两活塞间气体的体积为300m3,当气温升到T时把销子拔去。若刚拔去销子时两活塞的加速度大小为1.2m/s2,方向水平向左,求温度T为多少?(设大气压强为1.0![]() 105Pa不变,容器内气体温度始终和外界气温相同)
105Pa不变,容器内气体温度始终和外界气温相同)
【答案】325K
【解析】两活塞间理想气体,初状态:P1=P0,T1=250K
末状态P2 ;T2=T
由理想气体状态方程: ![]()
将两活塞和杆作为研究对象,由牛顿第二定律:P2SA+P0SB-P0SA-P2SB=(M+m)a
联立解得:T=325K

练习册系列答案
相关题目
【题目】跳水运动员从10m高的跳台上跳下(不计一切阻力),在下落的过程中( )
A. 运动员的动能减少,重力势能增加
B. 运动员的动能增加,重力势能减少
C. 运动员克服重力做功
D. 运动员的机械能在减少
【题目】在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速![]() ,已知
,已知![]() 时刻,波刚好传播到
时刻,波刚好传播到![]() 处,如图所示,在
处,如图所示,在![]() 处有一接收器(图中未画出),则下列说法正确的是 。
处有一接收器(图中未画出),则下列说法正确的是 。

A.波源开始振动时方向沿y轴负方向 |
B.从 |
C.接收器在 |
D.若波源向x轴正方向运动,接受器接收到波的频率可能为 |
E.若该波与另一列频率为![]() 沿x轴负方向传播的简谐横波相遇,不能产生稳定的干涉图样
沿x轴负方向传播的简谐横波相遇,不能产生稳定的干涉图样