题目内容
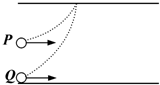 如图所示,质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射入两平行板间的匀强电场中.P从两极板正中央射入,Q从下极板边缘处射入,它们最后打在同一点(重力不计),则从开始射入到打到上板的过程中( )
如图所示,质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射入两平行板间的匀强电场中.P从两极板正中央射入,Q从下极板边缘处射入,它们最后打在同一点(重力不计),则从开始射入到打到上板的过程中( )分析:将两个带电粒子的运动垂直电场方向和平行电场方向正交分解,垂直电场方向不受力,做匀速直线运动;平行电场方向受到电场力,做初速度为零的匀加速直线运动,根据运动学公式、牛顿第二定律和功能关系联合列式分析.
解答:解:A、垂直电场方向即水平方向带电粒子不受力,做匀速直线运动,位移相等,速度相等,则运动时间相等,故A错误;
B、C平行电场方向粒子做初速度为0的匀加速直线运动,满足:
y=
at2 即:a=
①
根据牛顿第二定律,有:qE=ma…②
由①②两式解得:q=
.所以它们所带的电荷量之比qM:qN=1:2,
电势能的减小量等于电场力做的功即△E=qEy,因为位移之比是1:2,电荷量之比是1:2,所以电场力做功之比为1:4,它们电势能减少量之比△EM:△EN=1:4.故B错误,C正确;
D、根据动量定理,有:动量增量△p=qEt,qP:qQ=1:2,t相等,则动量增量之比△pM:△pN=1:2,故D正确.
故选CD
B、C平行电场方向粒子做初速度为0的匀加速直线运动,满足:
y=
| 1 |
| 2 |
| 2y |
| t2 |
根据牛顿第二定律,有:qE=ma…②
由①②两式解得:q=
| 2ym |
| Et2 |
电势能的减小量等于电场力做的功即△E=qEy,因为位移之比是1:2,电荷量之比是1:2,所以电场力做功之比为1:4,它们电势能减少量之比△EM:△EN=1:4.故B错误,C正确;
D、根据动量定理,有:动量增量△p=qEt,qP:qQ=1:2,t相等,则动量增量之比△pM:△pN=1:2,故D正确.
故选CD
点评:本题关键将两个带电粒子的运动垂直电场方向和平行电场方向的分运动,然后结合运动学公式、牛顿运动定律和动量定理列式分析.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
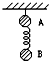 如图所示,质量相同的A、B两球用细线悬挂于天花板上且静止不动.两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间( )
如图所示,质量相同的A、B两球用细线悬挂于天花板上且静止不动.两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间( )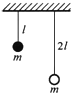 如图所示,质量相同的两个小球,分别用长l和2l的细线悬挂在天花板上.分别拉起小球使线伸直呈水平状态,然后轻轻释放,当小球到达最低位置时( )
如图所示,质量相同的两个小球,分别用长l和2l的细线悬挂在天花板上.分别拉起小球使线伸直呈水平状态,然后轻轻释放,当小球到达最低位置时( ) 如图所示,质量相同的木块A、B用轻弹簧相连,静止在光滑水平面上.弹簧处于自然状态.现用水平恒力F向右推A,则从开始推A到弹簧第一次被压缩到最短的过程中,下列说法中正确的是( )
如图所示,质量相同的木块A、B用轻弹簧相连,静止在光滑水平面上.弹簧处于自然状态.现用水平恒力F向右推A,则从开始推A到弹簧第一次被压缩到最短的过程中,下列说法中正确的是( )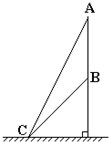 如图所示,质量相同的物体分别自斜面AC和BC的顶端由静止开始下滑,物体与斜面间的动摩擦因数都相同,物体滑到斜面底部C点时的动能分别为Ek1和Ek2,下滑过程中克服摩擦力所做的功分别为W1和W2,则( )
如图所示,质量相同的物体分别自斜面AC和BC的顶端由静止开始下滑,物体与斜面间的动摩擦因数都相同,物体滑到斜面底部C点时的动能分别为Ek1和Ek2,下滑过程中克服摩擦力所做的功分别为W1和W2,则( )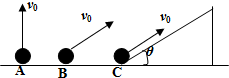 如图所示,质量相同的三个小球均可视为质点,处于同一水平面上.A球以初速度v0竖直上抛,B球以与水平面成θ角、大小也是v0的初速度斜向右上抛出,C球沿倾角为θ的足够长斜面以初速度v0上滑.上述运动过程中均不计空气阻力和一切摩擦,以下关于三个小球上升的最大高度的比较正确的是( )
如图所示,质量相同的三个小球均可视为质点,处于同一水平面上.A球以初速度v0竖直上抛,B球以与水平面成θ角、大小也是v0的初速度斜向右上抛出,C球沿倾角为θ的足够长斜面以初速度v0上滑.上述运动过程中均不计空气阻力和一切摩擦,以下关于三个小球上升的最大高度的比较正确的是( )