题目内容
如图是一高山滑雪运动场中的滑道,BD附近是很小的一段曲道,可认为是半径均为R=40m的两圆滑连接的圆形滑道,B点和D点是两圆弧的最高点和最低点,圆弧长度远小于斜面AD及BC长度,从A到D点不考虑摩擦力的作用。一个质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,从B点水平抛出时刚好对B点没有压力,已知AB两点间的高度差为h=25m,滑道的倾角θ=370,sin370=0.6,cos370=0.8,tan370=0.75取g=10m/s2。求:
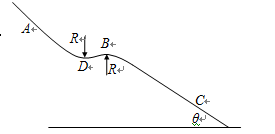
(1)运动员在B点时的速度。
(2)运动员在BC斜面的落点C到B点的距离(B点可认为是斜面上的最高点)。
(3)若BD之间的高度差为5m,AD段运动可看作直线动动,求运动员在D点对轨道的压力。

(1)运动员在B点时的速度。
(2)运动员在BC斜面的落点C到B点的距离(B点可认为是斜面上的最高点)。
(3)若BD之间的高度差为5m,AD段运动可看作直线动动,求运动员在D点对轨道的压力。
(1) (2)75m(3)1500N
(2)75m(3)1500N
 (2)75m(3)1500N
(2)75m(3)1500N本题考查平抛运动的分解运动,根据水平方向匀速运动和竖直方向自由落体的特点,由题意,在D点只受重力作用,重力提供向心力:
(1)运动员在B点时只受重力,根据牛顿第二定律有: ..............(2分)
..............(2分)
 解得:
解得: ...............................(1分)
...............................(1分)
(2)设运动员从B运动到C点的时间为t,根据平抛运动规律有:
运动员竖直位移为:y=gt2/2 (1).................................................(1分)
运动员水平位移为:x=vBt (2).................................................(1分)
由几何关系可知:tanθ=y/x (3).................................................(1分)
解(1)、(2)、(3)式得: t=3s.................................................(1分)
把t的值代入(2)式得: x=60m.................................................(1分)
所以BC的距离为:s=x/cosθ=75m.................................................(1分)
(3)运动员从A运动到D的过程中,根据牛顿第二定律有:
mgsinθ=ma ① (1分)

根据运动学规律有: ② (1 分)
运动员在D点时,根据牛顿第二定律有: ③(1分)
联立以上三式解得: FN=1500N (1分)
根据牛顿第三定律,所以运动员对D点的压力为1500N (1分)
(1)运动员在B点时只受重力,根据牛顿第二定律有:
 ..............(2分)
..............(2分) 解得:
解得: ...............................(1分)
...............................(1分)(2)设运动员从B运动到C点的时间为t,根据平抛运动规律有:
运动员竖直位移为:y=gt2/2 (1).................................................(1分)
运动员水平位移为:x=vBt (2).................................................(1分)
由几何关系可知:tanθ=y/x (3).................................................(1分)
解(1)、(2)、(3)式得: t=3s.................................................(1分)
把t的值代入(2)式得: x=60m.................................................(1分)
所以BC的距离为:s=x/cosθ=75m.................................................(1分)
(3)运动员从A运动到D的过程中,根据牛顿第二定律有:
mgsinθ=ma ① (1分)

根据运动学规律有: ② (1 分)
运动员在D点时,根据牛顿第二定律有: ③(1分)
联立以上三式解得: FN=1500N (1分)
根据牛顿第三定律,所以运动员对D点的压力为1500N (1分)

练习册系列答案
相关题目
 m C 10m D.
m C 10m D.  m
m





