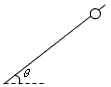题目内容
有一质量1kg小球串在长0.5m的轻杆顶部，轻杆与水平方向成θ=37°，静止释放小球，经过0.5s小球到达轻杆底端，试求
（1）小球与轻杆之间的动摩擦因数
（2）在竖直平面内给小球施加一个垂直于轻杆方向的恒力，使小球释放后加速度为2m/s2，此恒力大小为多少？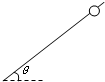
（1）小球与轻杆之间的动摩擦因数
（2）在竖直平面内给小球施加一个垂直于轻杆方向的恒力，使小球释放后加速度为2m/s2，此恒力大小为多少？
（1）小球沿杆做初速度为零的匀加速直线运动，所以有：
s=
at2 ①
根据牛顿第二定律得：mgsinθ-μmgcosθ=ma ②
联立①②得：μ=0.25
故小球与轻杆之间的动摩擦因数为μ=0.25．
（2）若F垂直杆向下，有：
mgsinθ-μ（F+mgcosθ）=ma
将a=2m/s2带入得：F=8N
若F垂直杆向上，有：
mgsinθ-μ（F-mgcosθ）=ma
同理带入数据得：F=24N．
故若F垂直杆向下F=8N，若F垂直杆向上F=24N．
s=
| 1 |
| 2 |
根据牛顿第二定律得：mgsinθ-μmgcosθ=ma ②
联立①②得：μ=0.25
故小球与轻杆之间的动摩擦因数为μ=0.25．
（2）若F垂直杆向下，有：
mgsinθ-μ（F+mgcosθ）=ma
将a=2m/s2带入得：F=8N
若F垂直杆向上，有：
mgsinθ-μ（F-mgcosθ）=ma
同理带入数据得：F=24N．
故若F垂直杆向下F=8N，若F垂直杆向上F=24N．
练习册系列答案
相关题目
（2011?兴宁区模拟）有一质量1kg小球串在长0.5m的轻杆顶部，轻杆与水平方向成θ=37°，静止释放小球，经过0.5s小球到达轻杆底端，试求
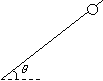
施加一个垂直于轻杆方向的恒力，使小球释放后加速度为2m/s2，此恒力大小为多少？
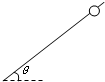有一质量1kg小球串在长0.5m的轻杆顶部，轻杆与水平方向成θ=37°，静止释放小球，经过0.5s小球到达轻杆底端，试求