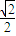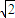题目内容
在地球表面某高度处以一定的初速度水平抛出一个小球,测得水平射程为s,在另一星球表面以相同的水平速度抛出该小球,需将高度降低一半才可以获得相同的水平射程.忽略一切阻力.设地球表面重力加速度为g,该星球表面的重力加速度为g′,
为( )
| g |
| g′ |
分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出时间,再根据水平初速度和时间求出位移,得出重力加速度的关系.
解答:解:根据h=
gt2得,t=
,则水平射程x=v0t=v0
.
因为初速度相等,x相等,高度变为原来的一半,则重力加速度变为原来的一半,即
=2.故D正确,A、B、C错误.
故选D.
| 1 |
| 2 |
|
|
因为初速度相等,x相等,高度变为原来的一半,则重力加速度变为原来的一半,即
| g |
| g′ |
故选D.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
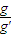 为( )
为( )
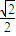
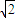
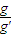 为( )
为( )