题目内容
(Ⅰ)如图为“用DIS(位移传感器、数据采集器、计算机)研究加速度和力的关系”的实验装置.
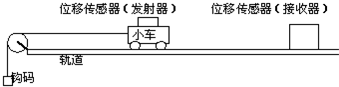
(1)在该实验中必须采用控制变量法,应保持 不变,用钩码所受的重力作为 ,用DIS测小车的加速度.
(2)改变所挂钩码的数量,多次重复测量.在某次实验中根据测得的多组数据可画出a-F关系图线(如图所示).
①分析此图线的OA段可得出的实验结论是 .
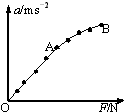
②(单选题)此图线的AB段明显偏离直线,造成此误差的主要原因是
A.小车与轨道之间存在摩擦 B.导轨保持了水平状态
C.所挂钩码的总质量太大 D.所用小车的质量太大
(Ⅱ)实验室新进了一批低电阻的电磁螺线管,课外活动小组的同学设计了一个试验来测算螺线管的电阻.他们选择了多用电表、电流表、电压表、开关、滑动变阻器、导线和学生电源等.
(1)他们使用多用电表粗测金属丝的电阻,操作过程分以下三个步骤:
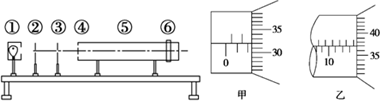
①将红表笔插入多用电表的 插孔(正、负)、黑表笔插入多用电表的插孔(正、负);选择电阻档“×1”;
②
③把红黑表笔分别与螺线管金属丝的两端相接,如图所示,读数为 Ω
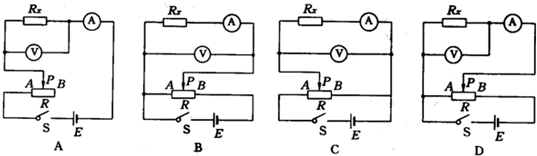
(2)根据多用电表示数,为了减少实验误差,并在实验中获得较大的电压调节范围,应从下图中的A、B、C、D四个电路中选择 电路来测量金属丝电阻;
(3)他们正确连接电路,接通电源后,调节滑动变阻器,发现电流始终无示数.请设计一种方案,利用多用电表检查电路故障并写出判断依据.(只需写出简要步骤)
①
② .

(1)在该实验中必须采用控制变量法,应保持
(2)改变所挂钩码的数量,多次重复测量.在某次实验中根据测得的多组数据可画出a-F关系图线(如图所示).
①分析此图线的OA段可得出的实验结论是

②(单选题)此图线的AB段明显偏离直线,造成此误差的主要原因是
A.小车与轨道之间存在摩擦 B.导轨保持了水平状态
C.所挂钩码的总质量太大 D.所用小车的质量太大
(Ⅱ)实验室新进了一批低电阻的电磁螺线管,课外活动小组的同学设计了一个试验来测算螺线管的电阻.他们选择了多用电表、电流表、电压表、开关、滑动变阻器、导线和学生电源等.
(1)他们使用多用电表粗测金属丝的电阻,操作过程分以下三个步骤:
①将红表笔插入多用电表的
②
③把红黑表笔分别与螺线管金属丝的两端相接,如图所示,读数为

(2)根据多用电表示数,为了减少实验误差,并在实验中获得较大的电压调节范围,应从下图中的A、B、C、D四个电路中选择

(3)他们正确连接电路,接通电源后,调节滑动变阻器,发现电流始终无示数.请设计一种方案,利用多用电表检查电路故障并写出判断依据.(只需写出简要步骤)
①
②
分析:I、解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项;该实验是探究加速度与力的关系,我们采用控制变量法 进行研究;根据图象得出变量之间的关系,知道钩码所受的重力作为小车所受外力的条件.
II、使用多用电表欧姆档测电阻时,要先估测待测电阻阻值,然后选择合适倍率,对欧姆表进行欧姆调零,最后用欧姆表测电阻,欧姆表读数是指针示数乘以倍率;待测电阻丝阻值很小,应该使用电流表的外接法;为了测出多组实验数据,且从零开始测量,滑动变阻器应使用分压接法,据此分析电路图,找出符合要求的实验电路;电流表无示数说明电路中有断路,电压表有示数说明电压表与电源连接的电路中无断路.
II、使用多用电表欧姆档测电阻时,要先估测待测电阻阻值,然后选择合适倍率,对欧姆表进行欧姆调零,最后用欧姆表测电阻,欧姆表读数是指针示数乘以倍率;待测电阻丝阻值很小,应该使用电流表的外接法;为了测出多组实验数据,且从零开始测量,滑动变阻器应使用分压接法,据此分析电路图,找出符合要求的实验电路;电流表无示数说明电路中有断路,电压表有示数说明电压表与电源连接的电路中无断路.
解答:解:I、(1)因为要探索“加速度和力的关系”所以应保持小车的总质量不变,钩码所受的重力作为小车所受外力;
故答案为:小车的总质量,小车所受外力.
(2)①由于OA段a-F关系为一倾斜的直线,所以在质量不变的条件下,加速度与外力成正比
②由实验原理:mg=Ma,得:a=
=
而实际上是:a′=
,可见AB段明显偏离直线是由于没有满足M>>m造成的,故ABD错误,C正确.
故答案为:①在质量不变的条件下,加速度与外力成正比,②C,
II、Ⅱ、(1)①红表笔和电表的“正”插孔相连,黑表笔和电表的“负”插孔相连.
②对欧姆表进行欧姆调零,具体操作是:将红黑表笔对接,调节欧姆调零电阻,使指针指在最右端零刻度线处;
③由图2(a)所示多用电表可知,欧姆表示数是4×1Ω=4Ω.
故答案为:①正,②将红、黑表笔短接,调整调零旋钮调零;③4.
(2)为减小误差,实验多次测量,根据题目要求可知,实验时应采用电流表的外接法,滑动变阻器应使用分压接法,由图2所是电路图可知,符合要求的实验电路是D.
故选D.
(3)①使用多用电表的电压档位,接通电源,逐个测量各元件、导线上的电压,若电压等于电源电压,说明该元件或导线断路故障.
②使用多用电表的电阻档位,断开电路或拆下元件、导线,逐个测量各元件、导线上的电阻,若电阻为无穷大,说明该元件或导线断路故障.
故答案为:①使用多用电表的电压档位,接通电源,逐个测量各元件、导线上的电压,若电压等于电源电压,说明该元件或导线断路故障;
②使用多用电表的电阻档位,断开电路或拆下元件、导线,逐个测量各元件、导线上的电阻,若电阻为无穷大,说明该元件或导线断路故障.
故答案为:小车的总质量,小车所受外力.
(2)①由于OA段a-F关系为一倾斜的直线,所以在质量不变的条件下,加速度与外力成正比
②由实验原理:mg=Ma,得:a=
| mg |
| M |
| F |
| M |
而实际上是:a′=
| mg |
| (M+m) |
故答案为:①在质量不变的条件下,加速度与外力成正比,②C,
II、Ⅱ、(1)①红表笔和电表的“正”插孔相连,黑表笔和电表的“负”插孔相连.
②对欧姆表进行欧姆调零,具体操作是:将红黑表笔对接,调节欧姆调零电阻,使指针指在最右端零刻度线处;
③由图2(a)所示多用电表可知,欧姆表示数是4×1Ω=4Ω.
故答案为:①正,②将红、黑表笔短接,调整调零旋钮调零;③4.
(2)为减小误差,实验多次测量,根据题目要求可知,实验时应采用电流表的外接法,滑动变阻器应使用分压接法,由图2所是电路图可知,符合要求的实验电路是D.
故选D.
(3)①使用多用电表的电压档位,接通电源,逐个测量各元件、导线上的电压,若电压等于电源电压,说明该元件或导线断路故障.
②使用多用电表的电阻档位,断开电路或拆下元件、导线,逐个测量各元件、导线上的电阻,若电阻为无穷大,说明该元件或导线断路故障.
故答案为:①使用多用电表的电压档位,接通电源,逐个测量各元件、导线上的电压,若电压等于电源电压,说明该元件或导线断路故障;
②使用多用电表的电阻档位,断开电路或拆下元件、导线,逐个测量各元件、导线上的电阻,若电阻为无穷大,说明该元件或导线断路故障.
点评:I、清楚实验的研究方法和实验中物理量的测量;当钩码的质量远小于小车的总质量时,钩码所受的重力才能作为小车所受外力.
II、本实验考查了实验操作、欧姆表读数等问题,熟练掌握基础知识,熟练应用欧姆定律、电阻定律即可正确解题.
II、本实验考查了实验操作、欧姆表读数等问题,熟练掌握基础知识,熟练应用欧姆定律、电阻定律即可正确解题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目